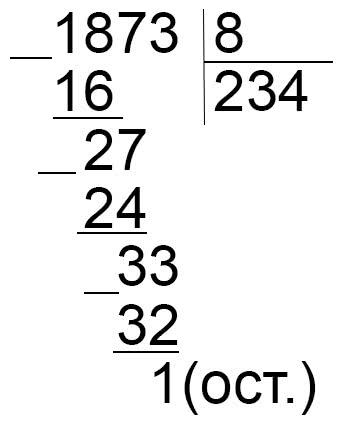Вычитание столбиком

Вычитание

Вычитание это процесс переноса числа по числовой прямой влево, то есть против движения числовой прямой. При этом результаты вычитания могут быть различны: может получиться ноль, положительное или отрицательное число.

Несмотря на то, что результаты вычисления могут быть различны, результат всегда остается в категории действительных чисел или комплексных чисел, в зависимости от того, какие числа участвовали в вычислении. При вычитании рациональных чисел никогда не получится иррациональное число, а при вычитании действительных – комплексное. Нужно внимательно следить за этим.

Вычитать столбиком можно только рациональные числа с любым знаком. Столбиком не получится подсчитать вычитание обычных дробей, но эта операция всегда представляется в виде вычитания целых чисел в числителе, поэтому таким способом можно вычислять и подобные выражения.

Вычитание столбиком из чисел, содержащих нули.

Опять же, разберем на примере:

Записываем числа в столбик. Которое больше — сверху. Начинаем вычитание справа налево по одной цифре. 9 — 3 = 6.

Из нуля вычесть 2 не получится, тогда опять занимаем у цифры слева. Это нуль. Ставим над нулем точку. И снова, у нуля занять не получится, тогда двигаемся дальше к следующей цифре. Занимаем у единицы. Ставим над ней точку.

Обратите внимание:
когда в вычитании столбиком над 0 есть точка, нуль становится девяткой. Над нашим нулем есть точка, значит, он стал девяткой

Вычитаем из нее 4. 9 — 4 = 5. Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0.
Полученный нуль не нужно записывать

Над нашим нулем есть точка, значит, он стал девяткой. Вычитаем из нее 4. 9 — 4 = 5
. Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0.
Полученный нуль не нужно записывать.

Скачать карточки

В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.

Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.

Понравился наш контент? Подпишитесь на канал в .

Принцип деления для детей

Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.

Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.

Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.

Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.

После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.

Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.

Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку»

Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Использование функций

Табличный процессор обладает мощным функционалом, поэтому пользователей интересует опрос, как считать в Excel. Приложение предлагает воспользоваться формулами. Распространенная формула: «=СУММ» – находит сумму введенных чисел.

Для нахождения результата пользователь:

• выбирает ячейку отображения результата;
• устанавливает курсор в строке формул;
• вводит функцию =сумм(диапазон ячеек);
• Нажимает «Enter».

Примечание: когда пользователь начинает вводить формулу, приложение выводит плавающую подсказку-справку. Здесь отображается, как должна выглядеть функция, какие должны быть аргументы. В конкретной функции в круглых скобках указывается диапазон подсчитываемых ячеек. Он либо вводится вручную, либо выделяется мышкой.

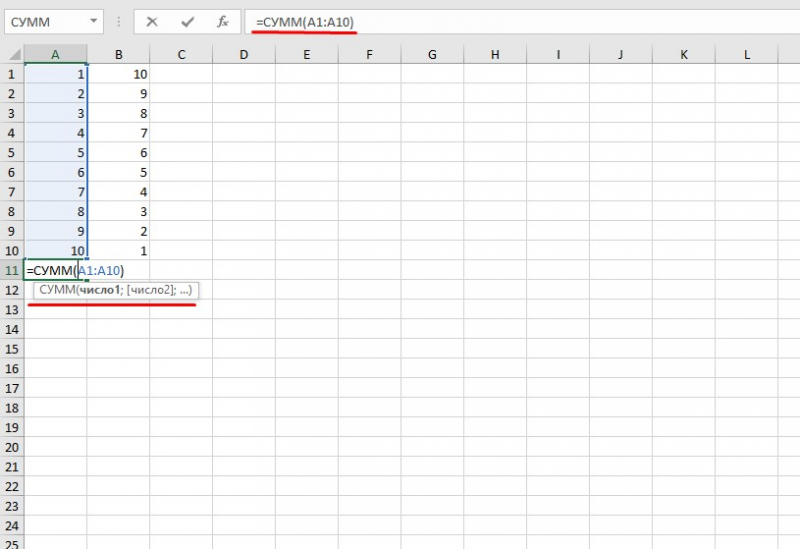
Сложение каждой ячейки

Для начала мы с вами научимся складывать просто несколько чисел, которые могут находиться в разных местах

Откройте документ excel, где у вас записаны какие-либо значения.
Теперь выберите какое-нибудь свободное место и поставьте туда знак «Равно» (=)

В этот момент у вас активировалась функция решения примеров, и неважно каких, сложения или вычитания.
Теперь нажмите на ячeйку, где у вас записано первое число, которое вы хотите использовать для сложения. В том месте, где мы ставили знак «=», должна появится координата этой цифры, т.е

C6 или D2, и т.д. Отлично. Это то, что нам нужно.
Теперь поставьте знак «+» и нажмите на следующую ячейкy с данными, которое вы хотите использовать для сложения. Видите, как меняется значение в том месте, где мы ставили «=»? Да. Теперь там стоят уже две координаты, объединенные плюсом.
Таким же образом продолжайте искать оставшиеся цифры и когда они закончатся, вам останется нажать Enter и значения, которые вы выбрали суммируются, а сама сумма покажется в ячейке, в которой мы изначально ставили знак равенства.

Как научить ребёнка считать до 100

Расскажите ребёнку о том, что десятков всего девять, после этого назовите каждый десяток: десять, двадцать, тридцать и так далее. Предложите ему каждый день заучивать по 10 новых цифр каждого десятка. В конце дня спрашивайте, что ребёнок запомнил и повторяйте то, что он выучил в другие дни. Упростить повторение можно считая предметы, которые находятся перед вами. После того как ребёнок освоит десятки, предложите ему сыграть в игру: напишите ряд чисел с десятками и пропустите одно число в середине, попросив ребёнка вписать в этом месте пропущенное число.

Также можно использовать методику Глена Домана. Сначала ребёнку нужно показывать карточки с количеством точек не более пяти, затем с большим количеством точек — 20, 50 и далее до 100. Этот метод поможет также натренировать зрительную память.

Многозначные числа

Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:

1. Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
2. Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.

При обучении решению задач с крупными числами действуйте поэтапно:

1. Объясните, что такое неполное делимое и зачем его выделять.

2. Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:

Найдите неполное частное в примерах: 369:28; 897:12; 698:36.

1. Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
2. Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.

106’8:89

1. Подбирайте частное на отдельном листочке или посчитайте в уме.
2. Распишите результат.
3. Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
4. Продолжайте деление до конца, пока не получится 0.
5. Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

Что делать, если разделить нужно десятичную дробь?

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Как вычитать столбиком

Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков — десятки и т. д. Результат вычитания записывают под чертой:

Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого:

От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц:

В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:

Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу:

При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 .

Теперь рассмотрим вычитание столбиком из чисел, содержащих нули:

Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен:

Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. Из 10 вычитаем 5, пишем 5:

В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354:

Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так:

А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило:

Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9.

Суммирование

Суммирование – важная операция, необходимая для подсчета данных в различных сферах. Если с нахождением суммы диапазона не возникает вопросов, как посчитать сумму ячеек в Excel, если даны одно или несколько условий.

Сумма с одним условием

Дана задача, при которой нужно подсчитать сумму ячеек при выполнении конкретного условия. Здесь пользователь применяет функцию, аналогичную фильтру значений. Проверка выполняется в:

Текстовое значение

Для решения задачи с одним условием в виде текстового значения юзер:

• создает таблицу;
• выбирает ячейку, где будет подсчитана сумма, и устанавливает курсор в строку формул;
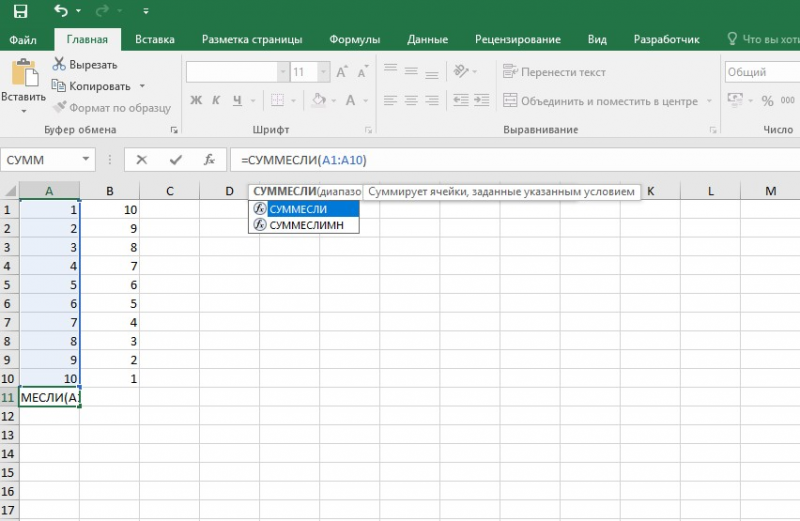
• вводит команду: =суммесли (условия выполнения).
• последовательно указывает диапазон значений, условие отбора, диапазон суммирования.
• для получения результата нажимает «Enter». В выбранной ячейке указывает сумму тех значений, которые удовлетворяют поставленному условию.

Примечание: Первый параметр – диапазон значений, среди которых будет проводиться отбор.

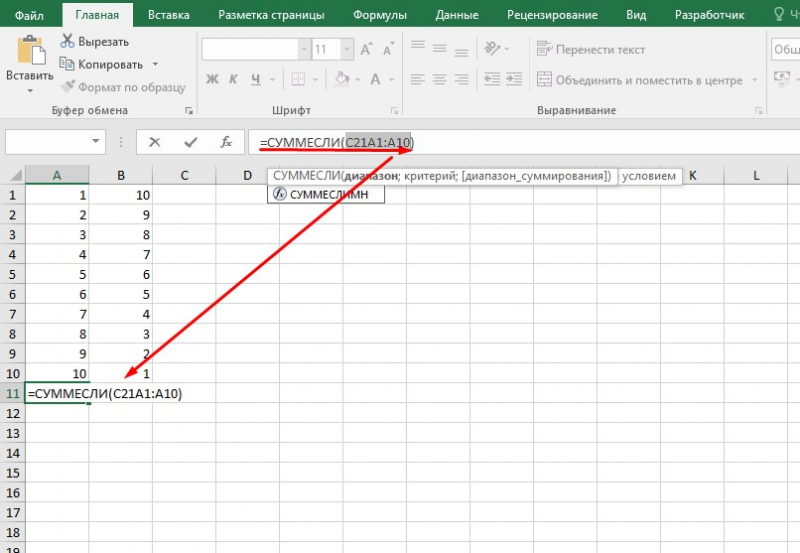
Второй параметр – критерий, указывающий, что нужно искать.

Третий параметр – диапазон суммирования, из которого будут выбираться значения, удовлетворяющие второму параметру, и складываться.

Критерий отбора указывается в кавычках.

Между параметрами функции обязательно должен быть разделитель «;» (точка с запятой). В противном случае приложение выдаст ошибку о неверно написанной функции.

После введения формулы нужно обязательно проверить правильность расстановки скобок.

Численное значение

Для получения суммы с одним условием в численном формате пользователь:

• формирует таблицу;
• выбирает ячейку, где будет отображаться итог решения задачи;
• переходит в строку формул;
• вписывает функцию: =суммесли (условия выполнения);
• действует согласно предыдущему алгоритму, указывая условия отбора и диапазоны значений;
• для получения результата нажимает «Enter». В выбранной ячейке указывается сумма тех значений, которые удовлетворяют поставленному условию.

Сумма с несколькими условиями

Иногда юзеру нужно решить задачу, где указаны 2 и более условий, и нужно найти сумму значений, удовлетворяющих заданным критериям. Для этого используется функция «=СУММЕСЛИМН»

Поэтому важно знать, как в Экселе сделать сумму с несколькими условиями. Для этого пользователь:

• формирует таблицу по заданному образцу;
• выбирает ячейку, где будет отображаться итог решения задачи;
• переходит в строку формул;
• вписывает функцию: =суммеслимн (условия выполнения).
• последовательно указывает диапазон сложения, диапазон условия1, условие1 и т.д.;
• для получения результата нажимает «Enter». В выбранной ячейке указывает сумма тех значений, которые удовлетворяют поставленному условию.

Примечание: Первый параметр – диапазон сложения, из которого будут выбираться значения, удовлетворяющие условиям, и складываться.

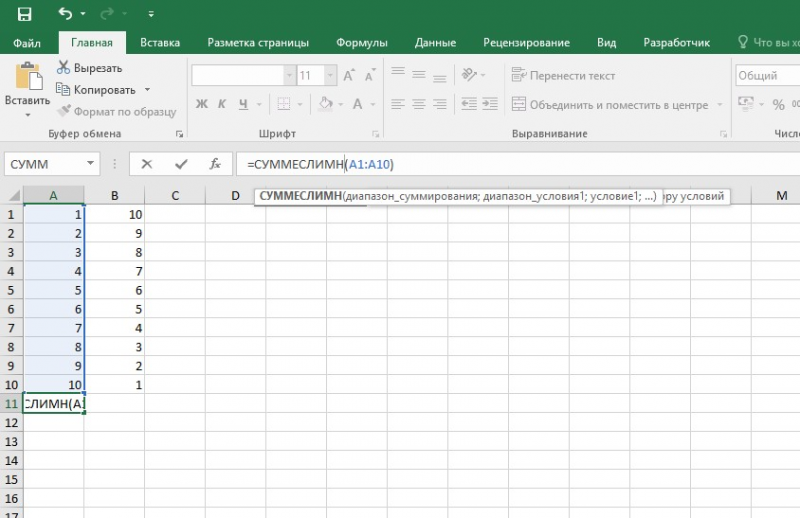
Второй параметр – диапазон условия 1, указывающий столбец, в котором проходит фильтрация по первому условию.

Третий параметр – условие1, которое указывается в кавычках и задает фильтрацию.

Четвертый и последующий параметры аналогичны второму и третьему, т.е. диапазон условия2, условие2; диапазон условия3, условие3 и т.д.

Условий отбора может множество.

Между параметрами функции обязательно должен быть разделитель «;» (точка с запятой). В противном случае приложение выдаст ошибку о неверно написанной функции.

После введения формулы нужно обязательно проверить правильность расстановки скобок.

Произведение двух столбцов

Возникают ситуации, когда нужно знать, как посчитать сумму в Excel через произведение двух столбцов. Для этого пользователь:

• вводит значения в 2 столбца;
• выбирает ячейку, где отображается результат;
• устанавливает курсор в строку формул и вводит текст:=сумм (диапазон ячеек одного столбца ) *сумм(диапазон ячеек другого столбца);
• для получения результата нажимает «Enter».

Примечание: при ручном написании функций важно проверить правильность расстановки скобок. В противном случае приложение выдаст сообщение об ошибке и предложит исправить недочет

Для получения произведения двух столбцов пользователь:

• находит сумму чисел в первом и втором столбце;
• в произвольной ячейке отмечает произведение двух сумм путем написания формулы в строке формулы или непосредственно в ячейке;
• нажимает «Enter».

Умножаем и делим, используя таблицу умножения

Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример:
4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082: 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Вычитание

Вычитание это процесс переноса числа по числовой прямой влево, то есть против движения числовой прямой. При этом результаты вычитания могут быть различны: может получиться ноль, положительное или отрицательное число.

Несмотря на то, что результаты вычисления могут быть различны, результат всегда остается в категории действительных чисел или комплексных чисел, в зависимости от того, какие числа участвовали в вычислении. При вычитании рациональных чисел никогда не получится иррациональное число, а при вычитании действительных – комплексное. Нужно внимательно следить за этим.

Вычитать столбиком можно только рациональные числа с любым знаком. Столбиком не получится подсчитать вычитание обычных дробей, но эта операция всегда представляется в виде вычитания целых чисел в числителе, поэтому таким способом можно вычислять и подобные выражения.

Деление на двузначное число

Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип:

1. Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
2. Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
3. Запишите ответ: 196:28 =6.

Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:

Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.
Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370

Важно начинать запись с первого числа слева.

После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
Теперь делим 370 на 74

Подбираем множитель (5) и записываем его под уголком.
Умножаем 5 на 74, записываем результат в столбик. Получится 370.
Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка. 4070:74=55. Частное смотрим под уголком.

Для проверки правильности решение произведите умножение: 74х55=4070.

Как вычитать десятичные дроби в столбик

При записи десятичных дробей нижние и верхние разряды чисел должны соотвествовать друг другу: целые под целыми, десятые под десятыми, сотые под сотыми, тысячные под тысячными

Действия с десятичными дробями производятся так же, как и с натуральными

Основные правила, которые важно знать при решении примеров на вычитание в столбик:

1. Сначала следует уравнять количество знаков после запятой. Это делается путём добавления нулей. Например, необходимо вычесть из дроби 5,5 число 2,03. Как видно из примера, количество знаков после запятой разное. Чтобы сделать их одинаковым, в дробь 5,5 (пять целых пять десятых) в конце добавляем ноль и получаем 5,50 (пять целых пятьдесят сотых). Это правило следует из правил вычитания простых дробей. Как известно, дроби с разными знаменателями нельзя складывать или вычитать. Прежде их необходимо привести в общему знаменателю. В приведённом примере десятичные дроби можно записать в виде 5 5/10 и 2 3/100. Из целых чисел нужно вычитать целые, из дробных — дробные. В примере знаменатели у дробей разные, наименьший общий знаменатель равен 100. Следовательно, числитель и знаменатель дроби 5/10 следует умножить на 10, в итоге получим 50/100, что в переводе в десятичную дробь будет выглядеть как 5,50.
2. Числа записать таким образом, чтобы запятая нижнего находилась в том же месте, что и у верхнего. Проще всего записывать числа, начиная с запятой. Поставить две запятые сверху и снизу, а затем уже расписывать знаки по обе стороны. Это правило, кстати, действует на основании того же правила вычитания простых дробей — из целого вычитаются целые, а из дробных — дробные. Запятая в результате должна располагаться точно под двумя верхними.
3. Выполнить действие, не обращая внимания на запятую. Вычитают десятичные дроби справа налево, то есть начиная с самой правой цифры после запятой.
4. Поставить в ответе запятую под запятой. Так мы сможем правильно отразить результат вычисления.

Вычитать нужно по цифрам разрядов: целые из целых, сотые из сотых и так далее

Как посчитать сумму в Excel

• 24 Июль, 2009 –
• Уроки Excel –
• Tags : сумма в excel, таблицы excel
• 76 Comments

Самая простая формула в Excel – это, пожалуй, сумма значений определенных ячеек.

Простейший пример: у вас есть столбец цифр, под ним должна стоять сумма этих цифр.

Выделяете ячейки со значениями, и еще одну пустую под ними, где должно будет расположиться значение суммы. И нажимаем на кнопку автосуммы.

Другой вариант-отмечаем ячейку, где должно быть значение суммы, нажимаем кнопку автосуммы.

область, значения которой будут просуммированы, выделяется и в ячейки суммы мы видим диапазон просуммированных ячеек. Если диапазон тот, который нужен, просто нажимаем Enter . Диапазон суммирующихся ячеек можно менять

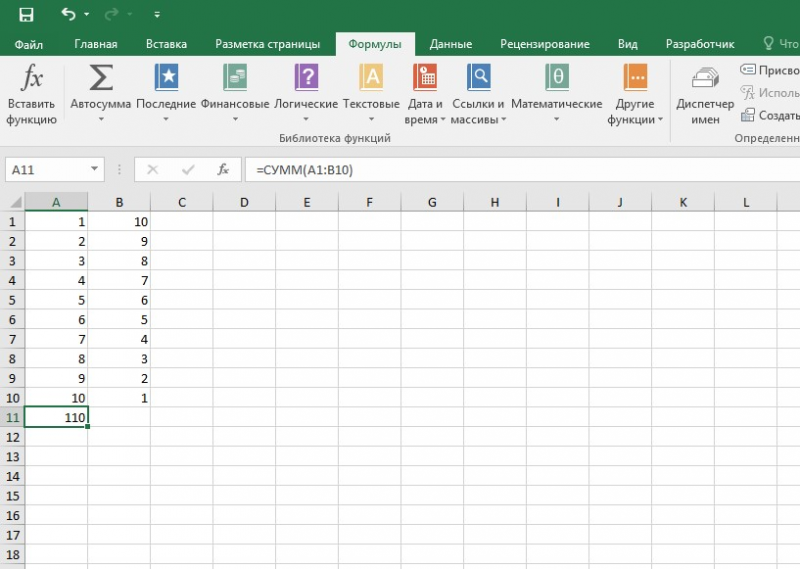
Например B4:B9 можно заменить на B4:B6 см.

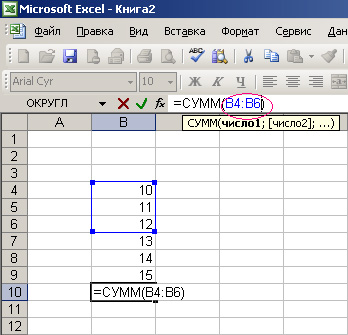
и мы получим результат

Теперь рассмотрим более сложный вариант.

Допустим, нужно сложить значения ячеек, которые не стоят в столбике подряд одно под другим. На рисунке желтым выделены ячейки, значения которых мы будем складывать.

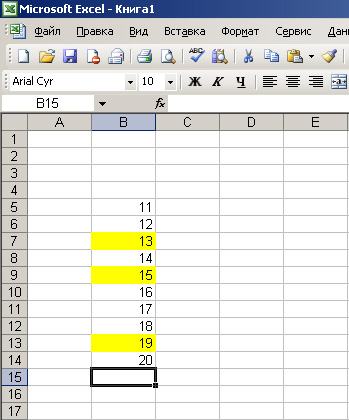
Ставим курсор на той ячейке, где должна быть сумма желтых ячеек. Жмем знак «равно», далее жмем на первую желтую ячейку, и в нашей ячейке суммы начинает формироваться формула. Дальше жмем знак «плюс»(+), за ним жмем на следующую желтую ячейку, затем снова «плюс», и последнюю желтую ячейку, на экране видим следующее:

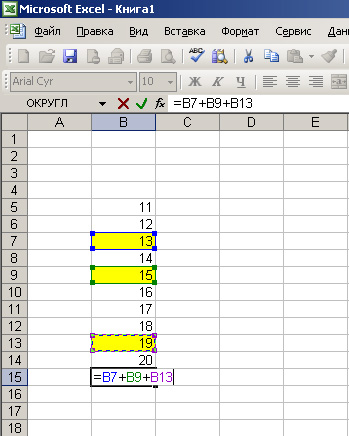
Дальше просто нажимаем Enter и вот мы получили сумму желтых ячеек.

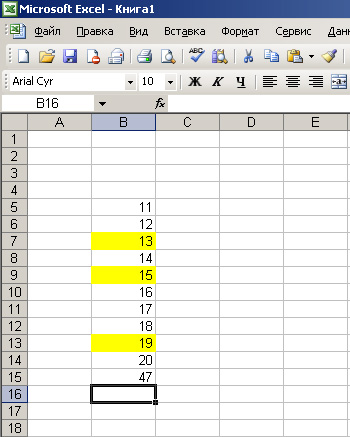
Бывает, что перед Вами не стоит задачи, чтобы в определенной ячейке стояло значение суммы ячеек. Допустим, Вам нужно быстренько посмотреть, какую сумму составляют несколько значений. В Excel и такое возможно

Воспользуемся старым примером с желтыми ячейками.

Внизу листа есть строка состояния. Сейчас там написано «Готово».

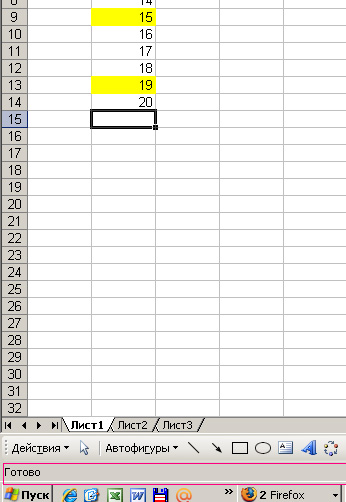
Если нажать правой мышью, появится меню, мы в нем выбираем значение «сумма»

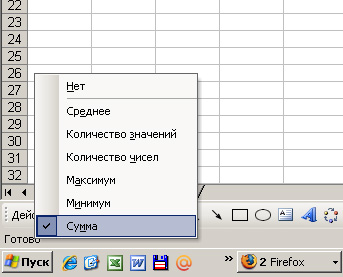
Теперь жмем на первую желтую ячейку, далее нажимаем и удерживаем на клавиатуре кнопку Ctrl и жмем на вторую желтую ячейку, и, продолжая удерживать C trl , жмем на третью желтую ячейку. В итоге мы видим на экране такую картину.

Обратите внимание, в правом нижнем углу появилось значение суммы желтых ячеек

Вычитание столбиком

Для того, чтобы вычесть столбиком два числа, нужно сначала правильно их записать. Два числа записываются друг под другом, так чтобы каждое число соответствовало своему разряду. То есть единицы записываются под единицами, десятки под десятками и так далее.

Если у числа имеется десятичная дробная часть, то она записывается по тому же принципу: десятые под десятыми, сотые под сотыми и так далее. Если вдруг получилось, что у одного числа есть сотые, а у другого их нет, то нужно просто во втором числе дописать нули для удобства вычисления. Два числа подчеркиваются, и под чертой пишется результат вычисления.

Сам процесс вычитания прост: из единиц уменьшаемого вычитаются единицы вычитаемого и так далее. То есть все вычитание разбивается на много вычитаний маленьких чисел не больше 9.

Приведем пример:

19590-13587

• Вычитаем единицы: 0-7 – вычесть единицы не получится, значит нужно единицу у следующего разряда. Значит, в следующем действии мы будем вычитать не из 9, а из 8. При этом 1 следующего разряда это 10 для настоящего. То есть, пример превращается в: 10-7=3
• По тому же принципу выполняем оставшиеся действия: 8-8=0
• 5-5=0
• 9-3=6
• 1-1=0 – десятков тысяч в записи не будет, так как получился ноль.
• Следующий шаг это правильная запись ответа, но при решении столбиком ответ получится сам собой: 6033

19590-13587=6033

Особое внимание нужно обращать на «займы» у следующих разрядов. В математике эта операция имеет название вычитания в столбик с переходом через десяток

Нужно понимать, что вычитая единицы, мы забрали 1 у разряда десятков. А 1 десяток это сколько 1? Верно, десять, так же как в 1 сотне 10 десятков и так далее. Понимание этого факта есть залог успешного вычитания.