Сложение и вычитание положительных и отрицательных чисел

Выведение аксиом для отрицательных чисел

Приняв приведенные выше утверждения, можно ответить на вопрос: «»Плюс» на «минус» дает какой знак?» Зная аксиому про умножение отрицательных чисел, необходимо подтвердить, что действительно (-C) х V = -(C х V). А также, что верно такое равенство: (-(-C)) = C.

Для этого придется вначале доказать, что у каждого из элементов существует лишь один ему противоположный «собрат». Рассмотрим следующий пример доказательства. Давайте попробуем представить, что для C противоположными являются два числа — V и D. Из этого следует, что C + V = 0 и C + D = 0, то есть C + V = 0 = C + D. Вспоминая о переместительных законах и о свойствах числа 0, можно рассмотреть сумму всех трех чисел: C, V и D. Попробуем выяснить значение V. Логично, что V = V + 0 = V + (C + D) = V + C + D, ведь значение C + D, как было принято выше, равняется 0. Значит, V = V + C + D.

Точно так же выводится и значение для D: D = V + C + D = (V + C) + D = 0 + D = D. Исходя из этого, становится ясно, что V = D.

Для того чтобы понять, почему все же «плюс» на «минус» дает «минус», необходимо разобраться со следующим. Так, для элемента (-C) противоположными являются C и (-(-C)), то есть между собой они равны.

Тогда очевидно, что 0 х V = (C + (-C)) х V = C х V + (-C) х V. Из этого следует, что C х V противоположно (-)C х V, значит, (-C) х V = -(C х V).

Для полной математической строгости необходимо еще подтвердить, что 0 х V = 0 для любого элемента. Если следовать логике, то 0 х V = (0 + 0) х V = 0 х V + 0 х V. А это значит, что прибавление произведения 0 х V никак не меняет установленную сумму. Ведь это произведение равняется нулю.

Зная все эти аксиомы, можно вывести не только, сколько «плюс» на «минус» дает, но и что получается при умножении отрицательных чисел.

Правила действий с отрицательными и положительными числами

Абсолютной величиной (или абсолютным значением) отрицательного числа называется
положительное число, получаемое от перемены его знака (-) на обратный (+). Абсолютная
величина -5 есть +5, т. е. 5. Абсолютной величиной положительного числа (а также числа ) называется само это число.

Знак абсолютной величины — две прямые черты, в которые заключается число, абсолютная величина которого берется. Например,

|-5| = 5,
|+5| = 5,
| 0 | = 0.

Сложение чисел с одинаковым знаком

сложении

Примеры.
(+8) + (+11) = 19;
(-7) + (-3) = -10.

б) При сложении двух чисел с разными знаками из абсолютной величины одного из них вычитается абсолютная величина другого (меньшая из большей) а ставится знак того числа, у которого абсолютная величина больше.

Примеры.
(-3) + (+12) = 9;
(-3) + (+1) = -2.

Вычитание (сложение) чисел с разными знаками

Вычитание

Примеры.
(+7) — (+4) = (+7) + (-4) = 3;
(+7) — (-4) = (+7) + (+4) = 11;
(-7) — (-4) = (-7) + (+4) = -3;
(-4) — (-4) = (-4) + (+4) = 0;

Замечание. При выполнении сложения и вычитания, особенно когда имеем дело с несколькими числами, лучше всего поступать так: 1) освободить все числа от скобок, при этом перед числом поставить знак « + », если прежний знак перед скобкой был одинаков со знаком в скобке, и « — », если он был противоположен знаку в скобке; 2) сложить абсолютные величины всех чисел, имеющих теперь слева знак +; 3) сложить абсолютные величины всех чисел, имеющих теперь слева знак -; 4) из большей суммы вычесть меньшую и поставить знак, соответствующий большей сумме.

Пример.
(-30) — (-17) + (-6) — (+12) + (+2);
(-30) — (-17) + (-6) — (+12) + (+2) = -30 + 17 — 6 — 12 + 2;
17 + 2 = 19;
30 + 6 + 12 = 48;
48 — 19 = 29.

Результат есть отрицательное число -29, так как большая сумма (48) получилась от сложения абсолютных величин тех чисел,
перед которыми стоили минусы в выражении
-30 + 17 – 6 -12 + 2.
На это последнее выражение можно смотреть и как на сумму чисел -30, +17, -6, -12, +2, и как на результат последовательного прибавления к числу -30 числа 17, затем вычитания числа 6, затем вычитания 12 и, наконец, прибавления 2. Вообще на выражение а — b + с — d и т. д. можно смотреть и как на сумму чисел (+а), (-b), (+с), (-d), и как на результат таких последовательных действий:
вычитания из (+а) числа (+b) , прибавления ( +c), вычитании ( +d) и т. д.

Умножение чисел с разными знаками

умножении

Схема (правило знаков при умножении):

+	*	+	=	+
+	*	—	=	—
—	*	+	=	—
—	*	—	=	+

Примеры.
( + 2,4) * (-5) = -12; 
(-2,4) * (-5) = 12; 
(-8,2) * (+2) = -16,4.

Примеры.
(+1/3) * (+2) * (-6) * (-7) * (-1/2) = -14 (три отрицательных сомножителя);
(-1/3) * (+2) * (-3) * (+7) * (+1/2) = 7 (два отрицательных сомножителя).

делении

Примеры.
(-6) : (+3) = -2;
(+8) : (-2) = -4; 
(-12) : (-12) = + 1.

Примеры сложения и вычитания целых чисел

Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.

Рассмотрим следующее простейшее выражение

1 + 3

Значение данного выражения равно 4

1 + 3 = 4

Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:

Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.

Пример 2. Найдём значение выражения 1 − 3

Значение данного выражения равно −2

1 − 3 = −2

Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:

Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.

Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.

Пример 3. Найти значение выражения −2 + 4

Значение данного выражения равно 2

−2 + 4 = 2

Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2

Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.

Пример 4. Найти значение выражения −1 − 3

Значение данного выражения равно −4

−1 − 3 = −4

Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4

Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.

Пример 5. Найти значение выражения −2 + 2

Значение данного выражения равно 0

−2 + 2 = 0

Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0

Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.

Тренажеры по математике 2 класс (задачи и примеры)

 В математике, конечно же, важно уметь думать и мыслить логически, но не менее важна в ней практика. Половина ошибок на экзаменах по математике делается из-за неправильного вычисления простых действий с числами – сложение, вычитание, умножение, деление

А отработать эти навыки важно еще в начальной школе. Чтобы ничего не упустить, необходимо систематически заниматься с ребенком по специальным тетрадям – тренажерам. Они позволяют отработать математические навыки и умения и довести их до автоматизма. Тренажеры разнообразные, не обязательно скачивать их все, достаточно одного-двух понравившихся. Пособия можно использовать в работе с младшими школьниками не зависимо от программы, по которой ведется обучение.

Один из самых важных моментов математики за 2 класс – отработать до автоматизма таблицу умножения. Отводим этой теме целую страницу. Чтобы перейти на нее и скачать тренажер на таблицу умножения, кликните по картинке:

Далее пособия расположены сверху вниз в порядке увеличения сложности. Чтобы посмотреть и скачать тренажер, кликните по обложке.

Математика. Решаем примеры с переходом через десяток.

Тетрадь для отработки навыков сложения и вычитания с переходом через десяток. Не просто примеры, а интересные игры и задания.

Карточки-задания. Математика. Сложение и вычитание. 2 класс

Удобные карточки для учителя второклашек. 2 варианта на сложение и вычитание одного вида. Подойдут для организации самостоятельной работы по математике в зависимости от продвижения по программе.

Математика. Сложение и вычитание в пределах 20. 1-2 классы. Е.Э.Кочурова

В разных курсах математике тема сложения и вычитание в пределах 20 изучается или в конце 1 класса, или в начале 2-го. В любом случае пособие поможет закрепить изученные способы манипуляций с числами, в некоторых заданиях эти способы представлены в виде своеобразных подсказок. В ходе самостоятельной работы с тетрадью ребенок ориентируется на образец выполнения и алгоритмические предписания. Умение пользоваться такими подсказками в учебе позволит ученику не только находить и использовать нужную информацию в ходе выполнения задания, но и осуществлять самопроверку. 

Начинается тетрадь с отработки навыков сложения и вычитание в пределах 10, эта часть подойдет и для первоклашек.

Математика тренажерная тетрадь для 2 класса

Тетрадь содержит не только примеры на сложение и вычитание, но и перевод единиц друг в друга, и сравнение результатов вычисления (больше-меньше).

3000 примеров по математике (счет в пределах 100 часть 1)

Тренажер со счетом на время. Время засекать на решение одной колонки примеров и записывать внизу в окошечке

Обратите внимание на колонки, которые ребенок решал более 5 минут, значит у него возникли сложности по этому виду примеров. Приведены примеры на сложение и вычитание в пределах десяти и с переходом через десяток,  сложение и вычитание десятков, манипуляции в пределах сотни

В этой прописи дается много примеров на сложение и вычитание, чтобы закрепить навыки устного счета в пределах 100.

Считаем правильно. Рабочая тетрадь по математике. Г.В.Белых

Тетрадь также выполнена в виде тренажера, сплошные примеры и уравнения.  Начинается со счета в пределах десяти, далее – в пределах сотни (сложение, вычитание, умножение и деление), заканчивается сравнением уравнений (примеры со знаками больше, меньше, равно).

Пособия пригодятся и учителям начальных классов в их работе, и родителям для занятий дома с детьми, в частности, в летние каникулы. Задания разных уровней сложности позволят осуществить дифференцированный подход к обучению.

А еще у нас есть отличный онлайн тренажер по математике! Родителям не нужно ничего распечатывать и проверять, все это за вас совершенно бесплатно сделаем мы! Выбирайте режим и вперед >>

Табличное сложение / Сложение / Справочник по математике для начальной школы

1. Главная

Справочники

Справочник по математике для начальной школы

Сложение

Табличное сложение

Прежде чем познакомиться с таблицами сложения чисел, мы рассмотрим случаи сложения разных видов.

Например, 7 + 6 = ?

Мы видим, что сумма будет больше 10, потому что 10 – это 7 и 3. Мы будем прибавлять число 6 по частям.

Сначала прибавляем столько, чтобы полу­чить 10:   7 + 3 = 10.

Дальше мы вспоминаем, что 6 — это 3 и 3.

Число 3 мы уже прибавили, значит, надо прибавить ещё 3:  10 + 3 = 13.

Тогда наш пример 7 + 6 можно записать по-другому: 

или так:

Значит, 7 + 6 = 13

Рассуждая так, можно решить любой пример на сложение в пределах 20.

Случаи табличного сложения

11 – это 1 и 10

11 – это 2 и 9

11 – это 3 и 8

11 – это 4 и 7

11 – это 5 и 6

12 – это 2 и 10

12 – это 3 и 9

12 – это 4 и 8

12 – это 5 и 7

12 – это 6 и 6

13 – это 3 и 10

13 – это 4 и 9

13 – это 5 и 8

13 – это 6 и 7

14 – это 4 и 10

14 – это 5 и 9

14 – это 6 и 8

14 – это 7 и 7

15 – это 5 и 10

15 – это 6 и 9

15 – это 7 и 8

16 – это 6 и 10

16 – это 7 и 9

16 – это 8 и 8

17 – это 7 и 10

17 – это 8 и 9

18 – это 8 и 10

18 – это 9 и 9

19 – это 9 и 10

Таблицы сложения

Таблица сложения нужна, чтобы научиться быстрому сложению чисел.

Существует несколько таблиц сложения чисел. Одна из первых таблиц такого рода – таблица сложения в пределах 10, но если ты хорошо знаешь состав чисел, тебе она не понадобится.

Как пользоваться такой таблицей?

Например, тебе нужно узнать, сколько будет 4 + 5.

Есть очень простая таблица сложения чисел с переходом через десяток. Вот она.

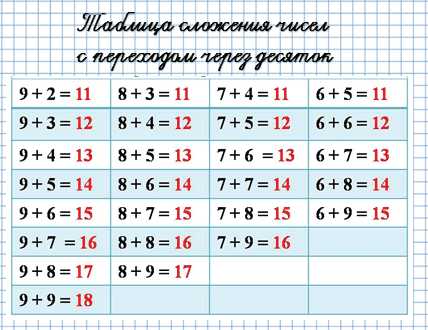
Пользоваться ею, конечно, очень легко.

Но наиболее полная таблица сложения чисел в от 1 до 20 представлена ниже.

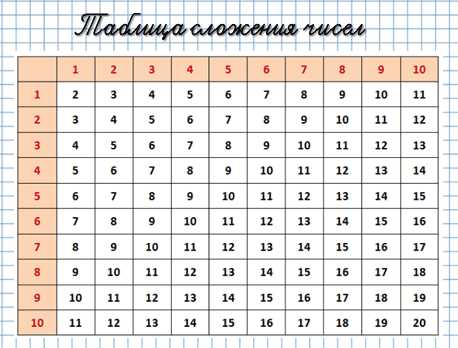
Как ею пользоваться? Очень просто.

Например, тебе нужно к 7 + 6:

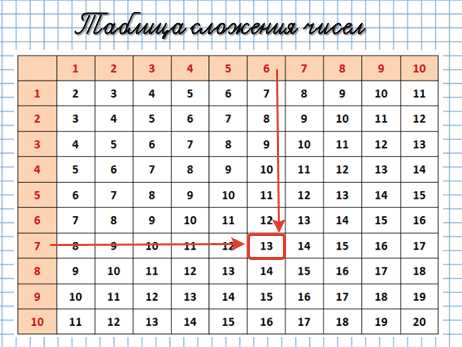
А это сводная таблица, которой можно прользоваться, пока не заучишь её наизусть.

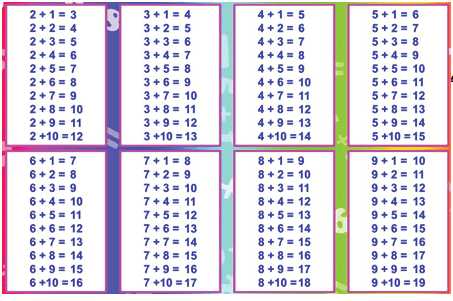
А такими таблицами можно пользоваться при заучивании результатов сложения наизусть.

Письменное сложение в столбик

Сложение

Правило встречается в следующих упражнениях:

1 класс

Страница 42. Вариант 1. № 1,

Волкова, Проверочные работы

Страница 70,

Моро, Волкова, Степанова, Учебник, 2 часть

Страница 73,

Моро, Волкова, Степанова, Учебник, 2 часть

Страница 79,

Моро, Волкова, Степанова, Учебник, 2 часть

Страница 86,

Моро, Волкова, Степанова, Учебник, 2 часть

Страница 94,

Моро, Волкова, Степанова, Учебник, 2 часть

Страница 35,

Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 40,

Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 45,

Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 46,

Моро, Волкова, Рабочая тетрадь, 2 часть

2 класс

Страница 10,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 24,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Задание 74,

Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 92,

Моро, Волкова, Рабочая тетрадь, 1 часть

Задание 133,

Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 18. Вариант 1. № 2,

Моро, Волкова, Проверочные работы

Страница 18,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 65,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 49,

Моро, Волкова, Рабочая тетрадь, 2 часть

Страница 75,

Моро, Волкова, Рабочая тетрадь, 2 часть

3 класс

Страница 6,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 8,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 23,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 37,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 65,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть

Страница 4,

Моро, Волкова, Рабочая тетрадь, 1 часть

Страница 5. Вариант 2. № 1,

Моро, Волкова, Проверочные работы

Страница 6,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 14,

Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть

Страница 12,

Моро, Волкова, Рабочая тетрадь, 2 часть

2019 – budu5.com, Буду отличником!

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:
−50 + 40

Решение
−50 + 40 = −10

Задание 2. Найдите значение выражения:
25 + (−5)

Решение
25 + (−5) = 20

Задание 3. Найдите значение выражения:
−20 + 60

Решение
−20 + 60 = 40

Задание 4. Найдите значение выражения:
20 + (−8)

Решение
20 + (−8) = 12

Задание 5. Найдите значение выражения:
30 + (−50)

Решение
30 + (−50) = −20

Задание 6. Найдите значение выражения:
27 + (−19)

Решение
27 + (−19) = 8

Задание 7. Найдите значение выражения:
−17 + (−12) + (−8)

Решение

Задание 8. Найдите значение выражения:
−6 − 4

Решение
−6 − 4 = −6 + (−4) = −10

Задание 9. Найдите значение выражения:
−6 − (−4)

Решение
−6 − (−4) = −6 + 4 = −2

Задание 10. Найдите значение выражения:
−15 − (−15)

Решение
−15 − (−15) = −15 + 15 = 0

Задание 11. Найдите значение выражения:
−11 − (−14)

Решение
−11 − (−14) = −11 + 14 = 3

Задание 12. Найдите значение выражения:
−3 + 2 − (−1)

Решение

Задание 13. Найдите значение выражения:
−5 − 6 − 3

Решение

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Сложение и вычитание отрицательных чисел

Рассмотрим в отдельности каждую из операций, чтобы не вызывать лишних вопросов.

Сложение отрицательных чисел

Сложение может происходить между:

• Двумя отрицательными числами.

  В этом случае минус выносится за знак скобок, числа складываются, а затем минус возвращается на место.

• Отрицательным и положительным числом. В этом случае, слагаемые меняются местами и получается обычная операция вычитания положительных чисел.
• Положительным и отрицательным числом. Согласно правилу знаков: «плюс на минус будет минус», а значит путем такого преобразования сложение превращается в вычитание положительных чисел.

Вычитание отрицательных чисел

Вычитание может происходить между:

• Двумя отрицательными числами. В этом случае «минус на минус» дает плюс. После этого, мы увидим выражение из предыдущего пункта, то есть сложение отрицательного числа с положительным. Нужно поменять числа местами и выполнить вычитание.
• Отрицательным и положительным числом. В этом случае получается та же ситуация, что при сложении двух отрицательных чисел. Так как, минус на плюс дает минус. Получившиеся числа складываются по модулю, а потом к результату возвращают минус.
• Положительным и отрицательным числом. Этот случай больше прочих любим составителями примеров. В результате преобразования по правилу знаков: «минус на минус» дает плюс. Значит, получится сложение двух положительных чисел.

Стоит добавить, что сложение или вычитание нуля никак не повлияет на отрицательное число. При этом, если из нуля вычесть число, то оно изменит свой знак на противоположный.

Что мы узнали?

Мы поговорили о том, что такое отрицательное число. Выяснили, чем отличается сложение и вычитание отрицательных чисел, и подробно расписали каждый из возможных случаев.

1. Вопрос 1 из 10

Начать тест(новая вкладка)

Как найти «удаленку» мечты: советы эксперта

Если вы хорошенько взвесили все «за» и «против» и точно решили, что готовы работать дистанционно, то вам наверняка пригодятся некоторые рекомендации от нашего эксперта Юлии Холодионовой:

• когда просматриваете вакансии, убедитесь в том, что в описании указаны не только требования к потенциальному кандидату, но и положенные ему компенсации;
• не пугайтесь собеседования в онлайн-формате. Напротив — такое интервью дает вам отличную возможность продемонстрировать, что вы готовы к такого рода сотрудничеству, и видеоконференция для вас — обычное дело. При личном общении обязательно соблюдение масочного режима и социальной дистанции;
• заранее почитайте отзывы о своем потенциальном работодателе, в том числе ознакомьтесь со списком нарушителей трудовых прав сотрудников;
• если удалось договориться, при трудоустройстве следите за тем, чтобы все ваши права были обозначены в трудовом договоре.

Удачи!

Права работника на дистанционной работе

Наш эксперт рассказывает, что, несмотря на расхожее заблуждение, удаленка, по сути своей, мало чем отличается от работы в офисе.

Многие считают, что рабочий день дистанционного сотрудника длится практически бесконечно. На самом деле это совсем не так. Существует четко определенное время, которое он обязан быть на связи и быть готовым отвечать руководителю в мессенджерах или по электронной почте. В остальные часы сотрудник имеет полное право не выходить на связь. Если же от человека требуют оставаться в Сети постоянно и без перерыва отвечать на сообщения, то это может быть расценено как принуждение к сверхурочной работе, что должно оплачиваться дополнительно.

Помимо нормированного рабочего дня дистанционный работник имеет следующие права:

право на перерыв в течение рабочего дня, продолжительность которого зависит от графика и продолжительности трудового дня;
право на ежегодный оплачиваемый отпуск, причем важно знать, что в этот период работодатель не в праве беспокоить сотрудника по рабочим делам. Ему положены отпускные, а сам он должен заранее уведомить руководство о своих планах

При возвращении к своим трудовым обязанностям необходимо сообщить об этом через корпоративную почту или мессенджеры;
работа «дистанционщика» ровно так же, как и его коллег в офисе, засчитывается в трудовой стаж;
работа на дому требует определенных затрат, например на Интернет и электроэнергию. Дистанционный работник имеет право потребовать компенсацию понесенных расходов. Для работодателя это означает появление некоторых новых денежных трат, однако это может оказаться даже выгоднее, нежели, например, закупать форму или оплачивать обеды.

Желательно, чтобы эти пункты были прописаны в локальном нормативном акте, а затем и в дополнительном соглашении к трудовому договору. Если изначально подразумевается, что удаленная трудовая деятельность будет носить временный характер, то все права и льготы должны быть закреплены в трудовом соглашении.

Если говорить о том, как оформить весь процесс с юридической точки зрения, то Юлия Холодионова рассказывает, что работодатель обязан ознакомить дистанционщика со всеми документами посредством электронных видов связи. Для данного вида коммуникации принято два специальных термина

1. Документ в электронном виде, который печатается на компьютере и оформляется в текстовом редакторе соответствующим образом, а затем отправляется для ознакомления заинтересованному лицу.
2. Электронный образец документа представляет собой вариант, отсканированный с бумажного носителя и заверенный электронной цифровой подписью.

Для того, чтобы подписать трудовое соглашение или договор о материальной ответственности, либо внести в них какие-либо изменения, необязательно ехать в офис. Все необходимые бумаги можно подписать, не выходя из дома, при помощи усиленной квалифицированной или неквалифицированной электронной цифровой подписи. Обе разновидности равноценны собственноручно поставленному «автографу». Также возможно применение иных способов взаимодействия, если таковые прописаны в коллективном договоре, локальном нормативном акте или дополнительном соглашении к трудовому договору.

Таблица сложения и вычитания | Учимся дома

Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать и  распечатать.

Таблица сложения до 20 распечатать и скачать

Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.

Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word.

Таблица сложения.rtf

Таблица сложения.pdf

Таблица вычитания до 20 распечатать и скачать

В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.

Таблица вычитания без ответов распечатать и скачать

Для проверки знания детей и их умения вычитать, можно использовать таблицу вычитания, в которой приведены возможные комбинации примеров. Таблицу вычитания без ответов можно распечатать и дать ребенку для заполнения правильными ответами.

Таблица вычитания без ответов.rtf

Таблица вычитания без ответов.pdf

На основе материалов   print.paint-net.ru

Общие математические правила

Конечно, такое объяснение не подойдет для школьников младших классов, которые только начинают учить абстрактные отрицательные числа. Им лучше объяснять на видимых предметах, манипулируя знакомым им термином зазеркалья. Например, придуманные, но не существующие игрушки находятся именно там. Их и можно отобразить со знаком «-». Умножение двух зазеркальных объектов переносит их в еще один мир, который приравнивается к настоящему, то есть в результате мы имеем положительные числа. А вот умножение абстрактного отрицательного числа на положительное лишь дает знакомый всем результат. Ведь «плюс» умножить на «минус» дает «минус». Правда, в младшем школьном возрасте дети не слишком-то пытаются вникнуть во все математические нюансы.

Хотя, если смотреть правде в глаза, для многих людей даже с высшим образованием так и остаются загадкой многие правила. Все принимают как данность то, что преподают им учителя, не затрудняясь вникать во все сложности, которые таит в себе математика. «Минус» на «минус» дает «плюс» – об этом знают все без исключения. Это верно как для целых, так и для дробных чисел.

Плюсы и минусы удаленной работы

Итак, мы выяснили, что притеснять сотрудников, которые по решению руководства были переведены на удаленку, трудовой кодекс не позволит и за ними закреплены все те же права, что и у офисных работников, и к тому же положены некоторые компенсационные выплаты.

Теперь пришла пора поговорить о достоинствах и недостатках такой формы организации труда.

Наш эксперт говорит, что чаша весов может склоняться в ту или другую сторону сообразно уровню мотивированности человека и в зависимости от особенностей его психики.

Среди очевидных плюсов Юлия Холодионова выделяет следующие:

• у вас не будет нужды в ежедневных визитах в офис;
• с большой долей вероятности удастся сэкономить на покупке деловых костюмов и туфель;
• съесть комплексный обед теперь можно на любимой кухне, не потратив на него несколько сотен рублей;
• ваш домашний Интернет и даже какую-то часть электроэнергии теперь будет оплачивать работодатель;
• теперь вам не придется тратить два-три, а то и больше часов из жизни на толкотню в переполненном транспорте;
• на дистанционке гораздо проще избегать конфликтов в коллективе. Если ваши отношения с коллегами трудно назвать теплыми, то этот вариант для вас идеален.

Но, конечно, есть и свои минусы:

• довольно скоро вы можете ощутить, что вам не хватает обратной связи с руководством и коллегами;
• ваши старания на удаленке оценить сложнее;
• вполне вероятно, у вас могут возникнуть сложности с овладением новыми компетенциями;
• не всем хватает самодисциплины, чтобы не отвлекаться на телевизор или Интернет, в итоге выполнение привычных обязанностей занимает больше времени;
• продуктивно трудиться могут помешать перебои с домашним Интернетом или неполадки с техникой — айтишника-то рядом нет;
• могут возникать проблемы с получением той или иной срочной информации.

Сложение двузначных чисел

Сложение двузначных чисел это всем привычный процесс, который можно выполнить в столбик или посчитать строкой «в уме». Но при этом можно считать быстро и в строку.

Рассмотрим пример: 18+29 – посчитаем сначала единицы, а затем десятки, после чего сложим результаты. Похожий подход используют при вычислениях в столбик.

9+8=17

10+20=30

30+17=47 – такой расчет займет меньше минуты, что сэкономит время для решения куда более важных задач.

Этот вариант наиболее универсален, но бывают ситуации, когда можно еще больше увеличить скорость счета. Наиболее любимый составителями примеров вариант: единицы двузначных чисел в сумме дают 10.

18+12=10+10+(8+2)=30 – просто к сумме десятков двух чисел прибавляется 1

Еще один вариант это два числа, которые ученикам психологически сложно считать. Не известно почему, но некоторые сложения тяжело даются учащимся.

Как правило, это: 7+6 и 8+7. Со временем ребята привыкают к тому, что первое равняется 13, а второе 15. Но лучше заучить это и не забивать голову.

Используются эти знания примерно так: 17+16=10+10+7+16=20+13=33

Заключение

Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма. 

Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.

Предыдущая
МатематикаВектор — виды, свойства и операции над отрезками
Следующая
МатематикаКатеты прямоугольного треугольника — свойства, основные формулы и примеры решений