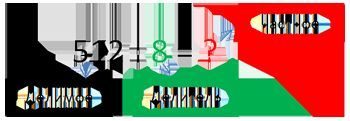
Примеры решения производных с ответами

Деление 4 класс

Курсы для развития интеллекта

Еще у нас есть интересные курсы, которые отлично прокачают Ваш мозг и улучшат интеллект, память, мышление, концентрацию внимания:

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать. После прохождения курса ребенок сможет:

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Если вы хотите разогнать свой мозг, улучшить его работу, подкачать память, внимание, концентрацию, развить больше креативности, выполнять увлекательные упражнения, тренироваться в игровой форме и решать интересные задачки, тогда записывайтесь! 30 дней мощного фитнеса мозга Вам гарантированы:)

Супер-память за 30 дней

Как только запишитесь на этот курс — для Вас начнется мощный 30-дневный тренинг развития супер-памяти и прокачки мозга.

В течение 30 дней после подписки Вы будете получать интересные упражнения и развивающие игры на свою почту, которые сможете применять в своей жизни.

Мы будем учиться запоминать все, что может потребоваться в работе или личной жизни: учиться запоминать тексты, последовательности слов, цифр, изображения, события, которые произошли в течение дня, недели, месяца и даже карты дорог.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Скорочтение за 30 дней

Вы бы хотели очень быстро прочитывать интересные Вам книги, статьи, рассылки и так далее.? Если Ваш ответ «да», то наш курс поможет Вам развить скорочтение и синхронизировать оба полушария головного мозга.

При синхронизированной, совместной работе обеих полушарий, мозг начинает работать в разы быстрее, что открывает намного больше возможностей

Внимание, концентрация, скорость восприятия усиливаются многократно! Используя техники скорочтения из нашего курса вы сможете убить сразу двух зайцев:

Научиться очень быстро читать
Улучшить внимание и концентрацию, так как при быстром чтении они крайне важны
Прочитывать в день по книге и быстрее заканчивать работу

Ускоряем устный счет, НЕ ментальная арифметика

Секретные и популярные приемы и лайфхаки, подойдет даже ребенку. Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Расчёт определителя

В математике линейной есть два понятия – определитель и детерминант. Определитель – это какое-либо число, которое ставится в соответствии с квадратной матрицей. Определитель используется при решении многих задач. Найти его можно с помощью формулы.

А детерминант находиться с помощью перемножения простых матриц, используются числа только с побочной и главной диагоналях.

Есть вероятность, что произведения матрицы будут значительно отличаться друг от друга. Если индекс чётный, то число будет со знаком плюс, если нечётный, то число будет со знаком минус. Обозначается определитель det А, а круглые скобки меняются на квадратные.

Пример 1

Дано

Решение

Пользуемся свойствам степеней – A^{3}=A^{2}*A

Возведём А в A^{2}

Далее используем свойство степеней

Ответ

Пример 2

Задание

Найдите определитель матрицы А.

Решение

Игры на развитие устного счета

Правила арифметики

Порядок выполнения операций в выражении – очень важен!

Если пример имеет вид 2+3-4, то порядок в нем может быть каким угодно. Потому что операции сложения и вычитания имеют одинаковый приоритет. Если выполним сначала сложение, то получим: 5-4=1, а если сначала вычитание, то: 2-1=1. Как видите результат одинаковый.

Аналогично с выражением умножения и деления. Операции умножения и деления имеют одинаковый приоритет. Например, 28:4. Выполним сначала умножение: 16:4=4, а если деление: 22=4.

Порядок имеет смысл, когда в выражении смешиваются операции сложения или вычитания, с операциями умножения или деления. Например:

2+22. Первым действием выполняются ВСЕ операции умножения и деления, а только потом сложения и вычитания. То есть выражение 2+22 = 2+4=6.

Но в выражениях присутствуют скобки. Скобки имеют свойство менять порядок операций. Рассмотрим предыдущий пример, только со скобками: (2+2)*2. В таком случае сначала выполняются операции в скобках, а затем вне скобок в порядке: 1. Умножение и деление 2. Сложение и вычитание.

Так, (2+2)2=42=8.

Как вы могли убедиться на примерах, скобки имеют роль. И порядок операций так же.

Придумывание задач

Обычно ребята, посещавшие детский сад, имеют представление о структуре задачи. Но видят сходство (похожесть) задач не все из них

Важно это вот почему. В школе на уроке ученики решают типовые задачи

Домой учитель задаёт похожую. Ребёнок, умеющий сравнивать, рассуждает: «Ага, мы такую задачку в школе решали. Только там было так и так, а здесь эдак». Задачка решается как знакомая. В противном случае она воспринимается как новая. Какую задачку проще решить: известную или новую?

Пример придумывания задачи

У нас есть выражение

3 + 4 = ?

Придумай по нему задачку. Можете дать образец, если не уверены, что чадо понимает, чего вы от него хотите.

Образец.

Условие. Мама дала 3 конфеты дочке и 4 конфеты сыну.

Вопрос. Сколько конфет было у мамы?

А теперь по этому же выражению ребёнок придумывает свою задачку. Меняйте только конфеты на игрушки, тарелки, печенье, зайцев, ёлки ….

Единственное запрещённое действие: нельзя складывать лампочки с апельсинами.

Надоело сложение, переходите к вычитанию. Маму с детьми на что-нибудь другое замените для разнообразия.

Матрицы и определители

Пример 1. Сумма матриц

Дано:
Матрицы A и B., Найти:
Сумму матриц A + B = C.C- ?

Решение:
Для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Таким образом, суммой двух матриц A и B является матрица:

Ответ:

Пример 2. Умножение матрицы на число

Дано:
Матрица
Число k=2.

Найти:
Произведение матрицы на число: A × k = BB — ?

Решение:
Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число.
Таким образом, произведение матрицы A на число k есть новая матрица:

Ответ:

Пример 3. Умножение матриц

Дано:
Матрица ;
Матрица .

Найти:
Произведение матриц: A × B = CC — ?

Решение:
Каждый элемент матрицы С = A × B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Строки матрицы А умножаем на столбцы матрицы В и получаем:

Ответ:

Пример 4. Транспонирование матрицы

Дано:
Матрица .

Найти:
Найти матрицу транспонированную данной.AT — ?

Решение:
Транспонирование матрицы А заключается в замене строк этой матрицы ее столбцами с сохранением их номеров. Полученная матрица обозначается через AT

Ответ:

Пример 5. Обратная матрица

Дано:
Матрица .

Найти:
Найти обратную матрицу для матрицы A.A-1 — ?

Решение:
Находим det A и проверяем det A ≠ 0:. det A = 5 ≠ 0.

Составляем вспомогательную матрицу AV из алгебраических дополнений A_ij: .

Транспонируем матрицу AV:.

Каждый элемент, полученной матрицы, делим на на det A:

Ответ:

Пример 6. Ранг матрицы

Дано:
Матрица .

Найти:
Ранг матрицы A.r(A) — ?

Решение:
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров M_k этой матрицы. Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.

Вычислим ранг матрицы, применив .

M3₂≠0;

.

Ответ: r(A) = 2

Пример 7. Определитель квадратной матрицы

Дано:
Матрица .

Найти:
Определитель |A| матрицы A.|A| — ?

Решение:
Каждой квадратной матрице А можно поставить в соответствие число, которое называется ее определителем и обозначается det А или |А|. Определитель матрицы третьего порядка вычисляется через ее элементы, по следующей формуле:
Тогда, для данной в примере матрицы A, определитель |A| будет равен:

Ответ: |A| = 16.

Пример 8. Минор и алгебраическое дополнение

Дано:
Матрица .

Найти:
Минор и алгебраическое дополнение элемента a₂₁ определителя |A| матрицы A.Δ₂₁ — ? A₂₁ — ?

Решение:
Запишем определитель матрицы A: .

Минор элемента a₂₁ определителя |A|- это определитель, который получится из данного вычеркиванием 2-й строки и 1-го столбца. Для минора используют обозначение Δ₂₁.

Алгебраическое дополнение A₂₁ элемента a₂₁ в определителе — это число, которое вычисляется по правилу: A_ij = (-1)i+j · Δ_ij, где Δ_ij — соответствующий минор. Тогда, подставив данные в формулу, получим:A₂₁ = (-1)2+1 · (-6) = 6.

Ответ: Δ₂₁ = -6; A₂₁ = 6.

Падежи существительных. Падежные предлоги

Именительный падеж

Именительный падеж упо­треб­ля­ет­ся для наиме­но­ва­ния пред­ме­тов. Это исход­ная, началь­ная фор­ма суще­стви­тель­но­го, кото­рая отве­ча­ет на вопро­сы:

• кто? — бабушк а , мастер , отец ;
• что? — тишин а , дом , счасть е , радость .

Именительный падеж все­гда упо­треб­ля­ет­ся без пред­ло­га и назы­ва­ет­ся пря­мым паде­жом в отли­чие от осталь­ных, нося­щих назва­ние кос­вен­ных. В име­ни­тель­ном паде­же суще­стви­тель­ное высту­па­ет в роли под­ле­жа­ще­го в пред­ло­же­нии или имен­ной части ска­зу­е­мо­го.

Вася — мой млад­ший брат .

Родительный падеж

• нет (кого?) бабушк и , мастер а , отц а ;
• нет (чего?) тишин ы , дом а , счасть я , радост и .

Все кос­вен­ные паде­жи (кро­ме пред­лож­но­го) могут упо­треб­лять­ся как с пред­ло­га­ми, так и без них, напри­мер:

нет (чего?) дома — оста­но­вил­ся (у чего?) у дома.

Предлоги уточ­ня­ют зна­че­ние паде­жей. Так, с роди­тель­ным паде­жом для обо­зна­че­ния отсут­ствия пред­ме­та, ука­за­ния места, при­чи­ны, цели упо­треб­ля­ют­ся пред­ло­ги:

Например:

• Дам (кому?) бабушк е , мастер у , отц у ;
• дам (чему?) тишин е , дому, счасть ю , радост и .

С датель­ным паде­жом упо­треб­ля­ют­ся пред­ло­ги:

• Подойти к мате­ри;
• посту­пить соглас­но пра­ви­лам;
• идти навстре­чу вет­ру;
• дей­ство­вать напе­ре­кор судь­бе.

Винительный падеж

Винительный падеж суще­стви­тель­но­го обо­зна­ча­ет объ­ект дей­ствия и отве­ча­ет на вопро­сы: кого? что?

• Вижу (кого?) бабушк у , мастер а , отц а ;
• вижу (что?) тишин у , дом , счасть е , радость .

С суще­стви­тель­ны­ми в фор­ме вини­тель­но­го паде­жа в зна­че­нии объ­ек­та, вре­ме­ни, места, уступ­ки упо­треб­ля­ют­ся пред­ло­ги:

• Вернуться спу­стя год;
• рас­ска­зать про орла;
• прой­ти сквозь пла­мя;
• пере­сту­пить через сту­пень­ку;
• вый­ти, несмот­ряна ливень.

Предлоги «в», «на», «за», «под» в фор­ме вини­тель­но­го паде­жа суще­стви­тель­но­го рас­кры­ва­ют направ­лен­ность на объ­ект дей­ствия:

Творительный падеж

• Горжусь (кем?) бабушк ой , мастер ом , отц ом ;
• любу­юсь (чем?) тишин ой , дом ом , счасть ем , радость ю .

С этим паде­жом в зна­че­нии сов­мест­но­сти, места, при­чи­ны упо­треб­ля­ют­ся пред­ло­ги:

• при­е­хать с дру­гом;
• парить над полем;
• оста­но­вить­ся перед вок­за­лом;
• поса­дить за домом;
• дей­ство­вать соглас­но с рас­по­ря­же­ни­ем;
• я вме­сте с бра­том;
• в свя­зи с непо­го­дой;
• прой­ти меж­ду ряда­ми.

Предложный падеж

Предложный падеж суще­стви­тель­но­го обо­зна­ча­ет объ­ект раз­мыш­ле­ний и отве­ча­ет на вопро­сы: о ком? о чём?

• забо­чусь о ком? о бабушк е , о мастер е , об отц е ;
• рас­ска­жу о чём? о тишин е , о дом е , о счасть е , о радост и .

Существительное в фор­ме пред­лож­но­го паде­жа, как гово­рит его назва­ние, упо­треб­ля­ет­ся толь­ко с пред­ло­га­ми:

Предложные фор­мы суще­стви­тель­ных обо­зна­ча­ют объ­ект дей­ствия или место:

Обратим вни­ма­ние, что оду­шев­лен­ные суще­стви­тель­ные отве­ча­ют на вопро­сы: кто? кого? кому? кем? о ком?

Неодушевленные суще­стви­тель­ные отве­ча­ют на падеж­ные вопро­сы: что? чего? чему? чем? о чём?

Системы линейных уравнений

Пример 9. Метод Крамера

Дано:
Система линейных уравнений

Найти:
Решение системы линейных уравнений методом Крамера.x₁, x₂, x₃— ?

Составляем матрицу B из свободных членов данной системы уравнений — матрицу-столбец свободных членов:

Решаем пример методом Крамера, используя .

Условие Δ ≠ 0 выполняется, значит система совместна и определена, причём единственное решение вычисляется по формулам Крамера:

Δ₁ — 1-й вспомогательный определитель системы, получается из Δ заменой 1-го столбца на столбец свободных членов:

Δ₂ — 2-й вспомогательный определитель системы, получается из Δ заменой 2-го столбца на столбец свободных членов:

Δ₃ — 3-й вспомогательный определитель системы, получается из Δ заменой 3-го столбца на столбец свободных членов:

Подставив полученные значения в формулы Крамера, находим неизвестные члены уравнения: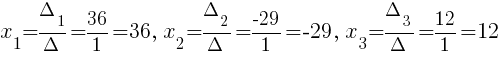

Ответ: .

Пример 10. Метод Гаусса

Дано:
Система линейных уравнений

Найти:
Решение системы линейных уравнений методом Гаусса.x₁, x₂, x₃— ?

Решение:
Составляем расширенную матрицу (A|B) системы из коэффициентов при неизвестных и правых частей:
(A|B)=

Приведём расширенную матрицу (A|B) системы к ступенчатому виду.

Из второй строки вычитаем первую строку, умноженную на четыре:
(A|B)~

Из третьей строки вычитаем первую строку, умноженную на два:
(A|B)~

Из третьей строки вычитаем вторую строку, умноженную на :
(A|B)~

Полученной диагональной матрице соответствует эквивалентная система: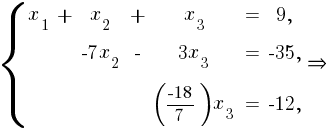

Ответ: .

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.

Теорема

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Алгоритм

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Логические задачи по математике для дошкольников и младших школьников с ответами

Задача двадцать первая

В комнате 4 угла. В каждом углу сидела кошка, напротив каждой кошки — 3 кошки. Сколько кошек находилось в комнате? (Ответ: 4 кошки)

Логические задачи для дошкольников по математике

Задача двадцать третья

Растет в поле елка. На елке 5 веток, на каждой ветке по 2 яблока. Сколько всего яблок на дереве? (Ответ: на елке яблоки не растут.)

Задача двадцать пятая

Во дворе гуляют куры и собаки, на всех 10 ног. Сколько во дворе кур и собак? (Ответ: 1 собака и 3 курицы или 2 собаки и одна курица.)

Интерес к математике можно развивать при помощи интересных игр, упражнений, задач. Желаем Вам удачи.

Смотрите далее:

• Уроки математики ребенку 6-7 лет
• Обучение детей математике 6-7 лет
• Самообразование игра

Развивающие математические игры для детей:

Отрицательное предложение. Примеры предложений:

С обычными глаголами

В английском языке, чтобы построить отрицательное предложение в Present Simple, нужны вспомогательные глаголы do и does. Они ставятся перед основным глаголом вместе с частицей not. Примеры:

• I work (я работаю) — I do not work (я не работаю).
• He reads (он читает) — He does not read (он не читает).

Когда употреблять do, а когда does?

Очень просто! Does используется с 3-м лицом ед.ч. (местоимениями he, she, it), а do — со всеми остальными.

Do not и does not очень часто сокращаются в разговорном английском. Do not имеет форму don’t, а does not — doesn’t.

Примеры отрицательных предложений в Present Simple с обычными глаголами:

Полная форма	Сокращенная форма	Перевод
I do not live in Moscow.	I don’t live in Moscow.	Я не живу в Москве.
He does not wear T-shirts.	He doesn’t wear T-shirts.	Он не носит футболки.
She does not play computer games.	She doesn’t play computer games.	Она не играет в компьютерные игры.
It does not look good.	It doesn’t look good.	Это не выглядит хорошо.
You do not like chocolate.	You don’t like chocolate.	Ты не любишь шоколад. / Вы не любите шоколад.
We do not go to the hospital.	We don’t go to the hospital.	Мы не ходим в больницу.
They do not buy books.	They don’t buy books.	Они не покупают книги.
Mike does not take music lessons.	Mike doesn’t take music lessons.	Майк не берет уроки музыки.
Kate and Jane do not argue.	Kate and Jane don’t argue.	Кейт и Джейн не ссорятся.
Vegetarians do not eat meat.	Vegetarians don’t eat meat.	Вегетарианцы не едят мясо.

С глаголом to be

Отрицания с глаголом to be образуются проще, чем с обычными глаголами. Мы просто добавляем частицу not после am, is, are. Примеры:

• I am a student (Я студент) — I am not a student (Я не студент).
• He is in Australia (Он в Австралии) — He is not in Australia (Он не в Австралии).

В разговорной речи отрицание с to be очень часто сокращается. Однако, у сочетания am not есть только один вариант сокращения. Примеры:

I am not sad. — I‘m not sad.

У сочетаний is not и are not есть два варианта сокращений. Примеры:

• He is not at school. — He isn’t at school / He‘s not at school.
• We are not cousins. — We aren’t cousins. / We‘re not cousins. 

Примеры отрицательных предложений в Present Simple с глаголом to be:

Полная форма	Сокращенная форма	Перевод
I am not a writer.	I’m not a writer.	Я не писатель.
He is not in the garden.	He isn’t in the garden.	Он не в саду.
She is not a cook.	She isn’t a cook.	Она не повар.
It is not on the table.	It isn’t on the table.	Это не на столе.
We are not Irish.	We aren’t Irish.	Мы не ирландцы.
They are not tired.	They aren’t tired.	Они не устали.
You are not responsible.	You aren’t responsible.	Ты не ответственный. / Вы не ответственные.
The car is not in the garage.	The car isn’t in the garage.	Машина не в гараже.
The lessons are not canceled.	The lessons aren’t canceled.	Уроки не отменены.
The UK is not very large.	The UK isn’t very large.	Великобритания не очень большая.

Вопросы и ответы. Примеры предложений:

С обычными глаголами

Чтобы образовать вопросы в Present Simple с обычными глаголами, мы также добавляем вспомогательные глаголы do и does. В данной статье мы рассмотрим два типа вопросов — общие и специальные.

Общие вопросы начинаются с do или does, в зависимости от лица (на русский язык do и does не переводятся). Такие вопросы требуют ответа «Да» или «Нет». Примеры:

• Do you speak English? (Вы говорите по-английски?) — Yes, I do. (Да) / No, I don’t. (Нет)
• Does he play tennis? (Он играет в теннис?) — Yes, he does. (Да) / No, he doesn’t. (Нет)

Специальные вопросы начинаются с вопросительных слов Where, What, When, Why, How и тд, а затем повторяют структуру общих вопросов. Пример:

When do you read books? (Когда ты читаешь книги?) — In the evening. (Вечером)

Отвечать на такие вопросы можно полным предложением или кратко. Пример:

Where does he play football? (Где он играет в футбол?) — He plays football on the stadium. (полный ответ) / On the stadium. (краткий ответ).

Примеры вопросительных предложений в Present Simple с обычными глаголами:

Вопрос	Перевод	Ответ	Перевод
Do you live in the city?	Ты живешь в городе? / Вы живете в городе?	Yes, I / we do. / No, I / we don’t.	Да / Нет
Does she play the piano?	Она играет на пианино?	Yes, she does. / No, she doesn’t.	Да / Нет
Does Tim sleep well?	Тим хорошо спит?	Yes, he does. / No, he doesn’t.	Да / Нет
Do they write letters?	Они пишут письма?	Yes, they do. / No, they don’t.	Да / Нет
Does he drive a car?	Он водит машину?	Yes, he does. / No, he doesn’t.	Да / Нет
Where do you live?	Где вы живете?	In Sydney.	Мы живем в Сиднее.
How do you make pasta?	Как ты готовишь пасту?	I use Mom’s recipe.	Я использую мамин рецепт.
What do you do in the morning?	Что ты делаешь утром?	I take a shower and make breakfast.	Я принимаю душ и готовлю завтрак.
Where does she go at 4 pm?	Куда она ходит в 4 часа дня?	To the swimming pool.	В бассейн.
What time do they go to sleep?	Во сколько они ложатся спать?	At 11 pm.	В 11 вечера.

С глаголом to be

С глаголов to be вопросы строятся простой перестановкой слов. Чтобы образовать общий вопрос, глаголы am, is, are ставятся вначале, то есть меняются порядком с подлежащим. Пример:

• He is a doctor. (Он врач.) — Is he a doctor? (Он врач?)
• They are builders. (Они строители.) — Are they builders? (Они строители?)

Специальные вопросы начинаются с вопросительных слов, а затем повторяют структуру общего вопроса. Пример:

• Why is he sad? (Почему он грустный?)
• When is your birthday? (Когда у тебя день рождения?)
• Where is the bag? (Где сумка?)

Примеры вопросительных предложений в Present Simple с глаголом to be:

Вопрос	Перевод	Ответ	Перевод
Are you on holiday?	Вы на каникулах? / Ты на каникулах?	Yes, we are. / No, we aren’t. / Yes, I am. / No, I am not.	Да / Нет
Is the apple red?	Яблоко красное?	Yes, it is. / No, it isn’t.	Да / Нет
Are they tall?	Они высокие?	Yes, they are. / No, they aren’t.	Да / Нет
Is Polly funny?	Полли смешная?	Yes, she is. / No, she isn’t.	Да / Нет
Are we happy?	Мы счастливы?	Yes, we are. / No, we aren’t.	Да / Нет
What color is the car?	Какого цвета машина?	It’s blue.	Она синяя.
How are you?	Как ты? Как дела?	I’m fine.	Хорошо.
Where is the post office?	Где почта?	It’s opposite the bank.	Она напротив банка.
Why are they tired?	Почему они устали?	They worked a lot.	Они много работали.
What time is your class?	Во сколько у тебя урок?	At 1 pm.	В час дня.

И напоследок, чтобы закрепить материал, советую вам посмотреть видео по всем трем видам предложений в Present Simple:

Успехов вам в изучении!

Читать далее:

Тест на Present Simple с ответами (для начинающих)Тест на Present Simple с ответами (для продолжающих)

Правила пунктуации со словом «например»

Для правильной постановки знаков препинания необходимо также принимать во внимание контекст и смысл фразы целиком:

1. Со значением уточнения, пояснения слово отделяется при помощи запятых с обеих сторон, если находится в середине предложения. При позиции в начале или в конце – одной запятой.
2. Слово «например» в начале обособленного оборота запятой от этого оборота не отделяется.
3. Когда обособленный оборот заключен в скобки, то запятая после «например» ставится.
4. Если за словом «например» следуют однородные члены предложения, впереди оно отделяется запятой, а после него ставится двоеточие.
5. В сочетании «как например» запятая не ставится в случае последующего перечисления.
6. Если перечисление отсутствует, то «например» выделятся запятыми с обеих сторон.

Примеры предложений

1. Завтра, например, ожидаются осадки.
2. Существуют разные виды спорта. Например, теннис.
3. Я люблю зелень. Петрушку, например.
4. В некоторых городах, например, в Сиднее, проходили Олимпийские игры.
5. В некоторых городах (например, в Сиднее) проходили Олимпийские игры.
6. Я посетил разные страны, например, Италию, Францию, Канаду, Тайланд.
7. Некоторые фрукты, как, например, лимон, апельсин, лайм… называются цитрусовыми.
8. Существуют гуманитарные дисциплины, как, например, история.

Векторная алгебра

Пример 11. Координаты вектора

Дано:
Точки: A(2, -4, 0); B(-4, 6, -2).

Найти:
Координаты вектора — ?

Решение:
Начало вектора совпадает с точкой А, конец – с точкой В. Находим координаты вектора :

Ответ:

Пример 12. Направляющие косинусы вектора

Дано:
Вектор: .

Найти:
Направляющие косинусы вектора . — ?

Решение:
Координаты вектора связаны с его направляющими косинусами следующим образом:

Ответ:

Дано:
Вектор: .

Найти:
Длину вектора . — ?

Решение:
Определяем длину вектора :

Ответ:

Пример 14. Объем параллелепипеда

Дано:
Координаты векторов:

Найти:
Объем параллелепипеда V — ?

Решение:
Объем параллелепипеда вычисляется по формуле:

Найдём смешанное произведение векторов:

Объем параллелепипеда:

Ответ: V=24.

Пример 15. Объем пирамиды

Дано:
Координаты векторов:

Найти:
Объем пирамиды V — ?

Решение:
Объем пирамиды вычисляется по формуле:

Найдём смешанное произведение векторов:

Вычисляем объём пирамиды:

Ответ: V=4.