Контрольная работа, самостоятельная работа, задачи по математике 3 класс

Контрольная работа по теме «Внетабличное умножение и деление»

Вариант 1

1. Найди частное и остаток.

10 : 3 =       8 : 5 =           6 : 4 =

2. Выполни деление в столбик

14 : 3         23 : 4       42 : 5           17 : 6         65 : 8

3. Сравни

6 м 8 дм … 68 дм                 45 мм … 4 см 5 мм

89 см … 9 дм 8 см               5 дм 4 см … 8 дм

4. Реши задачу

На одно платье идет 3 м ткани. Сколько платьев можно сшить из 17 м ткани? Сколько ткани останется?

5*. Найди лишнее слово в каждой строке и запиши его

а) метр, дециметр, килограмм, сантиметр

б) делимое, частное, делитель, множитель

в) март, октябрь, январь, зима, июнь

Вариант 2

1. Найди частное и остаток

9 : 4 =       7 : 2 =           8 : 3 =

2. Выполни деление в столбик

14 : 3         43 : 8       19 : 6           54 : 7         82 : 9

3. Сравни

38 дм …3 м 8 дм               37 мм … 4 см

68 см … 8 дм 6 см               5 м … 48 дм

4. Реши задачу

У Оли 15 рублей. Сколько булочек по 4 рубля она сможет купить? Сколько денег у неё останется?

5*. Найди лишнее слово в каждой строке и запиши его

а) ель, сосна, дерево, липа, берёза

б) сложение, уменьшаемое, деление, умножение

в) минута, час, сутки, утро, секунда

Что такое существительные третьего склонения?

В рус­ском язы­ке ряд слов жен­ско­го рода име­ет нуле­вые окончания:

• (что?) фасоль;
• она, моя фасоль (ж. р.);
• фасоль

Сравним:

• струч­ки (чего?) фасоли,
• лаком­люсь (чем?) фасолью

Такие сло­ва объ­еди­не­ны в тре­тий тип скло­не­ния имен суще­стви­тель­ных. Их мож­но узнать по мяг­ко­му зна­ку, кото­рый пишет­ся в кон­це после соглас­ных и всех шипя­щих соглас­ных, невзи­рая на их мяг­кость или твердость.

Например, бук­ва «ш» обо­зна­ча­ет все­гда твер­дый соглас­ный звук. Тем не менее у суще­стви­тель­ных тре­тье­го скло­не­ния все­гда после него пишет­ся мяг­кий знак, кото­рый не смяг­ча­ет его, а явля­ет­ся ука­за­те­лем при­над­леж­но­сти суще­стви­тель­но­го к тре­тье­му склонению.

• ветошь
• плешь
• рос­кошь

Примеры существительных 3 склонения

• вино­град­ная гроздь;
• непод­дель­ная радость;
• неожи­дан­ная новость;
• лес­ная рысь;
• забот­ли­вая мать;
• проч­ная трость;
• явная фальшь;
• едкая щёлочь;
• глу­хая полночь;
• таёж­ная глушь;
• бога­тая залежь минералов;
• вся помощь;
• яркая гуашь.

Составные задачи на увеличение числа на несколько единиц и в несколько раз

1. Засолили 6 кг белых грибов, подберёзовиков на 2 кг меньше, чем белых грибов, рыжиков в 2 раза больше, чем подберёзовиков. Сколько рыжиков засолили?2. У хомяка в одной кладовой 5 кг зерна, в другой на 3 кг больше, чем в первой, а в третьей в 2 раза меньше, чем во второй. Сколько килограммов зерна у хомяка в третьей кладовой?3. В аллее растёт 27 клёнов, берёз в 3 раза меньше, чем клёнов, а лип на 4 больше, чем берёз. Сколько лип растёт в аллее?4. За лето Марина прочитала 18 сказок, рассказов на 9 больше, чем сказок, а повестей в 9 раз меньше, чем рассказов. Сколько повестей прочитала за лето Марина?5. Тушканчику дают в сутки 3 г яйца, творога на 1 г больше, чем яйца, а моркови в 2 раза больше, чем творога. Сколько граммов моркови дают в сутки тушканчику?6. В вазе лежит 2 персика, груш на 2 больше, чем персиков, а слив в 3 раза больше, чем груш. Сколько слив лежит в вазе?7. Вера нарисовала 12 рисунков, Катя в 2 раза меньше, чем Вера, а Женя на 3 рисунка больше, чем Катя. Сколько рисунков нарисовала Женя?8. Дети собрали 10 кг чёрной смородины, белой в 2 раза меньше, чем чёрной, а красной на 9 кг больше, чем белой. Сколько килограммов красной смородины собрали дети?9. У Саши 7 видеокассет, у Коли на 2 видеокассеты больше, чем у Саши, а у Лёши в 3 раза больше видеокассет, чем у Коли. Сколько видеокассет у Лёши?10. В коробке 2 куска зелёного мела, белого в 9 раз больше, чем зелёного, а красного на 6 кусков меньше, чем белого. Сколько кусков красного мела в коробке?

Размер, метр, такт

Музыкальный размер показывает, сколько и каких долей включает в себя один такт. Выглядит размер как математическая дробь, где числитель — количество долей в такте, а знаменатель — длительность доли.

Число, расположенное сверху, говорит нам сколько долей содержит один такт; указывает до скольких нужно считать в каждом такте (до двух, до четырех, трех, шести и т.д.). при чтении это число принято называть в женском роде: две, четыре, три, шесть.

Число из нижней части дроби, обозначает длительность каждой доли; помогает понять, какими нотами следует считать удары пульса – четвертями, восьмыми и так далее. Это число произносят как соответствующее название длительности в родительном падеже: четверти, восьмых, шестнадцатых. Исключением будет размер, где счет осуществляется половинными нотами. Так размер 3/2 читается как «три вторых». А мы рассмотрим размер 2/4 «две четверти»:

Первая доля всегда сильная, она выделена красным цветом. Синим изображены слабые.

Метр

Очередность сильных и слабых долей называется метром.

Сильные и слабые доли чередуются в определённой последовательности, которую задаёт размер. Эта очередность долей создает метр произведения.

Такт

Отрезок музыки между двумя сильными долями называется тактом. На письме такты разделены вертикальными линиями — тактовыми чёрточками. Последний такт закрывается двумя тактовыми черточками.

Теперь, когда все элементы на месте, вы видите, что каждый такт соответствует размеру 2/4 и содержит по 2 четвертные доли.

Рассмотрим пример трехдольного размера – 3/4:

Первая доля — сильная. Размер указывает, что в одном такте должно быть 3 четвертные доли – значит вторая и третья будут слабыми.

Понятно188Запутался100

Составные задачи на нахождение стоимости

1. Купили 4 пирожка с вишней и 5 пирожков с творогом. Каждый из них стоит 20 копеек. Сколько денег заплатили за пирожки?2. Бабушка купила 4 м широкой тесьмы по 5 руб. и 3 м узкой тесьмы по 3 руб. Сколько денег заплатила бабушка за тесьму?3. Для аптечки купили 3 пачки ваты по 9 руб. и 4 бинта по 7 руб. Сколько стоит вся покупка?4. Хозяйка купила 10 кусков хозяйственного мыла по 3 руб. и 5 кусков детского мыла по 7 руб. Сколько денег заплатила хозяйка?5. Мама купила 8 йогуртов по 4 руб. и 2 фругурта по 10 руб. Сколько всего денег заплатила мама?6. Девочка купила 2 заколки для волос по 10 руб. и 4 резинки для волос по 2 руб. Сколько денег заплатила девочка?7. Купили 3 больших пакета по 7 руб. и 4 маленьких пакета по 3 руб. Сколько денег заплатили за пакеты?8. Оля купила 2 пачки «рожков» по 7 руб. и 3 пачки макарон по 10 руб. Сколько денег заплатила Оля?9. Мама купила 4 пачки фруктового мороженого по 7 руб. и 3 пачки шоколадного мороженого по 9 руб. Сколько денег заплатила мама за мороженое?10. Купили 2 губки для мытья посуды по 3 руб. и 4 мочалки для мытья посуды по 5 руб. Сколько денег заплатили за всё?

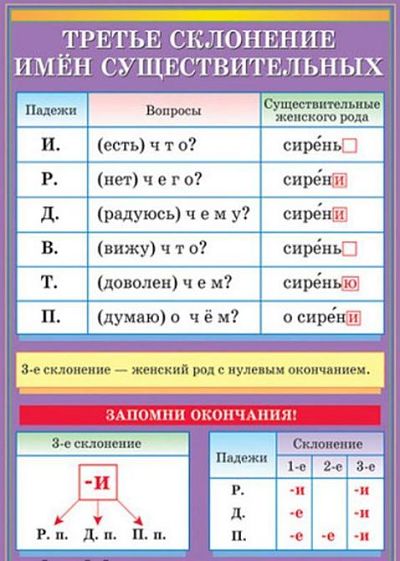
Изменение по падежам существительных 3 склонения

Рассмотрим, как изме­ня­ют­ся по паде­жам и чис­лам суще­стви­тель­ные тре­тье­го скло­не­ния. Для нагляд­но­сти соста­вим таб­ли­цу падеж­ных окон­ча­ний этих суще­стви­тель­ных в фор­мах един­ствен­но­го и мно­же­ствен­но­го числа.

Падежи	Вопросы	Ед. чис­ло	Мн. чис­ло
И. п.	(есть) что?	милость мелочь пустошь вещь	милости мелочи пустоши вещи
Р. п.	(нет) чего?	милости мелочи пустоши вещи	милостей мелочей пустошей вещей
Д. п.	(раду­юсь) чему?	милости мелочи пустоши вещи	милостям мелочам пустошам вещам
В. п.	(вижу) что?	милость мелочь пустошь  вещь	милости мелочи пустоши вещи
Т. п.	(дово­лен) чем?	милостью мелочью пустошью вещью	милостями мелочами пустошами вещами
П. п.	(думаю) о чём?	о милости о мелочи о пустоши о вещи	о милостях о мелочах о пустошах о вещах

Смешанные размеры

Смешанным называют сложный размер, который состоит из двух простых не одинаковых размеров – двухдольного и трехдольного. Чаще всего можно встретить размеры 5/4; 7/4 и 5/8; 7/8.

В опере Римского-Корсакова «Снегурочка», в заключительном хоре встречается размер 11/4. Размер причудливый, редкий. Чтобы музыкантам было легче просчитать и привыкнуть к нему, предлагают сперва потренироваться на фразе «Римский-Корсаков совсем с ума сошел». Эта фраза состоит из 11-ти слогов, которые соответствуют 11-ти долям. Фраза легко ложится на слух и после нее нотный текст разучить гораздо проще.

Размеры 5/4 и 5/8 – пятидольные. По своей сути они одинаковы, но в первом случае пульс шагает четвертями, во втором – восьмыми. Так как это сложный размер, он состоит из нескольких простых:

Если произведение написано в смешанном размере, то в скобках, как правило, указывают из каких простых размеров оно состоит. На изображении ниже, первый такт является суммой 2/4 + 3/4; второй – 3/4 + 2/4.

От того, как меняется последовательность простых размеров внутри сложного, зависит местоположение относительно сильной доли. В первом такте относительно сильной долей будет третья, во втором — четвертая. От расположения относительно сильной доли зависит акцент внутри такта, а значит и его ритмическая организация.

Размеры 7/4 и 7/8 – семидольные. Состоят из трех простых размеров, два из которых двухдольные и один трехдольный.

Трехдольный, как правило, используют в начале или в конце такта, реже — в середине. Несимметричные размеры чаще всего встречаются в музыке русских композиторов, а также в народной музыке. Неподготовленному слушателю трудно воспринимать такую музыку, однако, группа Pink Floyd сочинила песню «Money», мотив которой легко ложится на слух и запоминается.

Понятно — это просто186Совсем тяжко идет99

Математические диктанты. 3 класс.

Математика 3 класс1. 13 увеличить на 5.
2. 18 уменьшить на 6.3. Какое число надо увеличить на 9, чтобы получить 16?4. Найдите сумму чисел 9 и 7.5. Найдите разность 13 и 8.6. Запишите число, которое меньше 15 на 7.7. От какого числа надо отнять 5, чтобы получить 14.8. Петя решил 17 примеров, а Ваня на 5 примеров меньше. Сколько примеров решил Ваня?9. Напишите самое маленькое однозначное число.10. В одном отрезе 6 м материи, а в другом на 3 м больше. Сколько метров материи в двух отрезах?Математика 3 класс1 . 30 увеличить на 8,2. 68 уменьшить на 8.3. Сколько не хватает 13 до 27?4. От какого числа надо отнять 36, чтобы получить 12?5. Найди разность 53 и 6.6. Найдите сумму 50 и 24.7. Сколько будет 100 без 46?8. Первое слагаемое 45, второе 32. Найди сумму.9. К 73 прибавить 2 десятка.10. На первой полке 23 книг, на второй 19 книг. На третьей столько, сколько на первой и второй вместе. Сколько книг на третьей полке?Математика 3 класс1 . 86 увеличить на 8.2. Чему равна сумма 88 и 4?3. Первое слагаемое 35, второе 9. Чему равна сумма?4. К 74 прибавить 6.5. 42 уменьшить на 6.6. На сколько 33 больше, чем 9?7. Сколько нужно отнять от 62, чтобы получить 49?8. На сколько 29 меньше 43?9. В одном ящике 24 кг конфет, а в другом на 6 кг меньше. Сколько кг в двух ящиках?10. В двух классах 70 учеников. В одном классе 34 ученика. Сколько учеников во втором классе?Математика 3 класс1 . Найдите сумму 32 и 33.2. 96 увеличить на 4.3. Первое слагаемое 73, второе 17. Чему равна сумма?4. 86 уменьшить на 42.5. Сколько нужно добавить к 26 до 60?6. Сколько нужно отнять от 50, чтобы получить 27?7. Найдите разность 96 и 58. 8.100 без 72.9. Мальчик прочитал в первый день 18 страниц, а во второй на 8 страниц больше. Сколько всего страниц он прочитал за двадня?10. В одном ящике 28 кг яблок, во втором на 6 кг больше, а в третьем на 12 кг меньше, чем во втором. Сколько кг яблок в третьем ящике?Математика 3 класс1. 18 увеличить на 27.2. На сколько 56 больше 25?3. На сколько 37 меньше 91 ?4. Уменьшите 69 на 47.5. Найдите разность 80 и 41.6. Найдите сумму 45 и 36.7. Первое слагаемое 39, второе 61. Чему равна сумма?8. От сложения каких однозначных чисел получится 16?9. В одном классе 32 ученика, а в другом 29. На сколькобольше учеников в первом классе, чем во втором?10. У Люды в коллекции 70 календариков, а у Кати 39. На сколько меньше календариков у Кати, чем у Люды?Математика 3 класс1. 18 увеличить на 72.2. Найдите сумму 62 и 19.3. Из какого числа надо вычесть 23, чтобы получить 17?4. Что больше и на сколько: сумма 35 и 29 или разность 87 и 9?5. На сколько 90 больше 34?6. Уменьшаемое 62, вычитаемое 27. Найдите разность. 7. 17 увеличить на столько же.8. Запишите число, в котором цифра единиц на 3 больше цифры десятков.9. В одном куске 33 метра материи, а в другом на 17 метров меньше.Сколько материи в двух кусках?

Простые задачи на кратное сравнение

1. У причала стояло 18 катамаранов и 9 лодок. Во сколько раз больше у причала катамаранов, чем лодок?2. У Алиски 2 котёнка, а у Мурки 6 котят. Во сколько раз меньше котят у Алиски, чем у Мурки?3. На одной юбке 16 пуговиц, а на другой 8 пуговиц. Во сколько раз больше пуговиц на первой юбке, чем на второй?4. Купили 6 баранок с маком и 2 бублика. Во сколько раз меньше купили бубликов, чем баранок?5. В кофейном сервизе 6 чашек, а в чайном сервизе 12 чашек. Во сколько раз больше чашек в чайном сервизе, чем в кофейном?6. В зоопарке 10 зубров и 5 овцебыков. Во сколько раз меньше овцебыков, чем зубров?7. В одном оркестре 12 скрипок и 2 арфы. Во сколько раз больше в оркестре скрипок, чем арф?8. На детской площадке в парке играло 12 девочек и 4 мальчика. Во сколько раз меньше играло на площадке мальчиков, чем девочек?9. У Веры 16 листов цветной бумаги, а у Гены 8 листов. Во сколько раз больше листов цветной бумаги у Веры, чем у Гены?10. В комнате стояло 6 стульев и 2 кресла. Во сколько раз меньше кресел, чем стульев, стояло в комнате?

Диктант № 2. «Конкретный смысл умножение и деления»

1.Запиши выражения и вычисли их значения:

• Сумма двух слагаемых, каждое из которых равно 12.
• Сумма трёх слагаемых, каждое из которых равно 13.
• Сумма четырёх слагаемых, каждое из которых равно 14.
• Сумма пяти слагаемых, каждое из которых равно 15.

Решение:
12 + 12 = 24
13 + 13 + 13 = 39
14 + 14 + 14 + 14 = 56
15 + 15 + 15 + 15 + 15 = 75

2. Замени каждую сумму произведением и запиши соответствующие равенства.

Решение:
12 * 2 = 24
13 * 3 = 39
14 * 4 = 56
15 * 5 = 75

3. В каждом произведении переставь множители местами и запиши получившиеся равенства.

Решение:
2 * 12 = 24
3 * 13 = 39
4 * 14 = 56
5 * 15 = 75

4. По образцу: 16 * 6 = 96; 6 * 16 = 96; 96 : 6 = 16; 96 : 16 = 6 составь такие же равенства к полученным произведениям.

Решение:
24 : 2 = 12
24 : 12 = 2
39 : 3 = 13
39 : 13 = 3
56 : 4 = 14
56 : 14 = 4
75 : 5 = 15
74 : 15 = 5

Примеры по математике для 3 класса

Примеры по математике 3 класс

5 + 12 : 2	60 + 39 : 3 — 61
22 — 4 х 5	6 х 2 — 28 : 4
6 х (8 — 2)	9 х 4 + (71 — 17)
(54 + 9) : 9	24 + 6 х (5 — 2)
2 + 20 : 4	5 х (9 — 7) : 2
65 — 4 х 4	(51 + 9 х 3) : 6
9 х (9 — 2)	70 + 72 : 9 — 75
(21 + 9) : 3	9 х 8 + (45 — 22)
9 х 2 — 44 : 4	50 + 4 х (8 — 5)
5 х (7 — 4) : 3	(74 + 2 х 5) : 3

8 + 60 : 3	80 + 12 : 2 — 21
25 — 2 х 2	8 х 4 — 15 : 5
(67 + 3) : 2	4 х 5 + (82 — 71)
6 х (8 — 2) : 9	59 + 7 х (6 — 4)
5 + 80 : 8	(32 + 4 х 6) : 2
22 — 2 х 6	48 + 68 : 4 — 60
3 х (8 — 6)	7 х 9 — 15 : 5
(92 + 8) : 2	3 х 9 + (52 — 48)
3 х (8 — 2) : 9	58 + 3 х (6 — 2)
4 х 3 + 24 : 7	29 + 5 х 7) : 8

3 + 12 : 2	96 + 18 : 9 — 76
55 — 2 х 3	5 х 9 — 24 : 4
9 х (5 — 3)	7 х 5 + (80 — 55)
(41 + 3) : 4	85 + 3 х (6 — 2)
9 х (8 — 5) : 3	(64 + 4 х 8) : 2
4 + 40 : 8	74 + 24 : 3 — 75
48 — 5 х 9	3 х 4 — 54 : 9
4 х (4 — 2)	7 х 6 + (32 — 13)
(86 + 5) : 7	74 + 2 х (7 — 5)
5 х (6 — 4) : 2	(60 + 4 х 3) : 6

Примеры по математике 3 класс

4. Решите уравнения.

1) х : 8 = 9	2) 56 : y = 8	3) 7 * x = 49
4) x : 4 = 9	5) 8 * y = 32	6) 5 * z = 35

7) х * 8 = 72	8) 48 + y = 92	9) 15 — х = 13
10) х * 6 = 72	11) 81 — y = 19	12) 33 + х = 61
13) х * 13 = 39	14) 44 + y = 71	15) 52 — х = 14

1. Решите примеры:

1) 45 + 6 =	2) 18 — 8 =	3) 37 + 17 =
4) 67 + 4 =	5) 36 — 3 =	6) 48 + 23 =
7) 47 + 9 =	8) 35 — 9 =	9) 57 + 34 =

10) 31 + 8 + 9 + 42 =	11) 27 + 14 + 6 =	12) 46 + 7 + 13 =
13) 36 + 11 + 5 + 4 =	14) 75 + 8 + 5 =	15) 33 + 8 + 12 + 7 =
16) 32 + 5 + 8 + 33 =	17) 29 + 34 + 11 + 6 =	18) 18 + 25 + 2 + 5 =

Карточки по математике «Числовые выражения (все действия)» для учащихся 3 класса — Карточки с примерами — Развивайка — Обучение и развитие — ПочемуЧка

Задания — карточки по математике. Материал можно использовать для проверки навыков счёта в пределах 100 (составление программы действий, табличное умножение и деление, сложение и вычитание в пределах 100 с переходом через десяток). Предлагается 13 вариантов. Можно использовать для групповой работы. Дети выполняют задания на карточке.

1. РЕШИ ВЫРАЖЕНИЯ:

35 : 5 + 36 : 4 — 326 + 6 х 8 – 45 : 5 24 : 6 + 18 – 2 х 69 х 6 – 3 х 6 + 19 – 27 :3

2. РЕШИ ВЫРАЖЕНИЯ:

48 : 8 + 32 – 54 : 6 + 7 х 417 + 24 : 3 х 4 – 27 : 3 х 2 6 х 4 : 3 + 54 : 6 : 3 х 6 + 2 х 9100 – 6 х 2 : 3 х 9 – 39 + 7 х 4

3. РЕШИ ВЫРАЖЕНИЯ:

100 – 27 : 3 х 6 + 7 х 42 х 4 + 24 : 3 + 18 : 6 х 9 9 х 3 – 19 + 6 х 7 – 3 х 57 х 4 + 35 : 7 х 5 – 16 : 2 : 4 х 3

4. РЕШИ ВЫРАЖЕНИЯ:

32 : 8 х 6 : 3 + 6 х 8 – 175 х 8 – 4 х 7 + 13 — 11 24 : 6 + 18 : 2 + 20 – 12 + 6 х 721 : 3 – 35 : 7 + 9 х 3 + 9 х 5

5. РЕШИ ВЫРАЖЕНИЯ:

42 : 7 х 3 + 2 + 24 : 3 – 7 + 9 х 36 х 6 + 30 : 5 : 2 х 7 — 19 90 — 7 х 5 – 24 : 3 х 56 х 5 – 12 : 2 х 3 + 49

6. РЕШИ ВЫРАЖЕНИЯ:

32 : 8 х 7 + 54 : 6 : 3 х 550 – 45 : 5 х 3 + 16 : 2 х 5 8 х 6 + 23 – 24 : 4 х 3 + 1748 : 6 х 4 + 6 х 9 – 26 + 13

7. РЕШИ ВЫРАЖЕНИЯ:

42 : 6 + (19 + 6) : 5 – 6 х 260 – (13 + 22) : 5 – 6 х 4 + 25 (27 – 19) х 4 + 18 : 3 + (8 + 27) :5 -17(82 – 74) : 2 х 7 + 7 х 4 — (63 – 27): 48. РЕШИ ВЫРАЖЕНИЯ:

90 – ( 40 – 24 : 3) : 4 х 6 + 3 х 53 х 4 + 9 х 6 – ( 27 + 9 ) : 4 х 5(50 – 23) : 3 + 8 х 5 – 6 х 5 + ( 26 + 16) : 6(5 х 6 – 3 х 4 + 48 : 6) +(82 – 78) х 7 – 1354 : 9 + ( 8 + 19) : 3 – 32 : 4 – 21 : 7 + (42 – 14) : 4 – (44 14) : 5

9. РЕШИ ВЫРАЖЕНИЯ:

9 х 6 – 6 х 4 : (33 – 25) х 73 х (12 – 8) : 2 + 6 х 9 — 33 (5 х 9 — 25) : 4 х 8 – 4 х 7 + 139 х (2 х 3) – 48 : 8 х 3 + 7 х 6 — 34

10. РЕШИ ВЫРАЖЕНИЯ:

(8 х 6 – 36 : 6) : 6 х 3 + 5 х 97 х 6 + 9 х 4 – (2 х 7 + 54 : 6 х 5) (76 – (27 + 9) + 8) : 6 х 4(7 х 4 + 33) – 3 х 6 :2

11. РЕШИ ВЫРАЖЕНИЯ:

(37 + 7 х 4 – 17) : 6 + 7 х 5 + 33 + 9 х 3 – (85 – 67) : 2 х 5

12. РЕШИ ВЫРАЖЕНИЯ:

(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 х 5 – (60 – 42) : 3 + 9 х 2(9 х 7 + 56 : 7) – (2 х 6 – 4) х 3 + 54 : 9

13. РЕШИ ВЫРАЖЕНИЯ:

(8 х 5 + 28 : 7) + 12 : 2 – 6 х 5 + (13 – 5) х 4 + 5 х 4(7 х 8 – 14 : 7) + (7 х 4 + 12 : 6) – 10 : 5 + 63 : 9

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Математические матрицы»

«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Простые задачи деления по содержанию

1. 18 кг вишнёвого варенья разлили в банки по 3 л в каждую. Сколько понадобилось банок?2. 24 ломтика сала разложили на хлеб по 3 ломтика на каждый кусок хлеба. Сколько потребовалось кусков хлеба?3. 8 хомяков посадили в клетки по 2 хомяка в каждую клетку. Сколько клеток занято хомяками?4. 15 тетрадей разложили в папки по 3 в каждую. Сколько получилось папок?5. 8 самолётов стояли в ангарах по 4 в каждом. Сколько ангаров заняли самолёты?6. Мама испекла 24 пирожка. На каждом противне она пекла по 6 пирожков. Сколько противней с пирожками испекла мама? 7. 24 мяча разложили в коробки по 6 мячей в каждую. Сколько коробок с мячами получилось?8. 70 кг сена выдали коровам по 7 кг каждой. Сколько коров получили сено?9. На стройку привезли 24 т песка. Сколько машин привезли этот песок, если на каждой машине привезли по 8 т песка?10. 50 лампочек зажглось в гирляндах по 10 лампочек в каждой. Сколько новогодних гирлянд зажглось?

Составные задачи на разностное и кратное сравнение

1. Тётя Ира купила 3 кг моркови, а картофеля в 3 раза больше. На сколько килограммов больше купила тётя Ира картофеля, чем моркови?2. В магазин привезли 12 ящиков зелёных яблок, а красных в 2 раза меньше. На сколько меньше привезли ящиков красных яблок, чем зелёных?3. В детской комнате 2 стула, а в спальне в 3 раза больше. На сколько больше стульев в спальне, чем в детской комнате?4. В вагоне поезда ехало 30 взрослых пассажиров, а детей в 6 раз меньше. На сколько меньше в вагоне поезда было детей, чем взрослых?5. У портнихи 9 катушек белых ниток, а чёрных в 2 раза больше. На сколько меньше у портнихи катушек белых ниток, чем чёрных?6. В английской группе 14 учеников, а в немецкой в 2 раза меньше. На сколько больше учеников в английской группе, чем в немецкой?7. В доме 3 дивана, а кресел в 3 раза больше, чем диванов. На сколько меньше в доме диванов, чем кресел?8. У бабушки 4 сковородки, а кастрюль в 3 раза больше, чем сковородок. На сколько меньше у бабушки сковородок, чем кастрюль?9. У Оксаны 4 блузки, а у Карины в 2 раза больше. На сколько меньше блузок у Оксаны, чем у Карины?10. Папа съел 6 ломтиков колбасы, а мама в 3 раза меньше. На сколько ломтиков папа съел больше, чем мама?

Простые задачи на увеличение числа в несколько раз (косвенная форма)

1. В альбоме 10 фотографий об отдыхе на даче. Это в 2 раза больше, чем фотографий о летнем отдыхе на море. Сколько в альбоме фотографий об отдыхе на море?2. У Коли 27 фломастеров. Это в 3 раза больше, чем у Васи. Сколько фломастеров у Васи?3. Тётя Люся заготовила на зиму 12 банок клубничного компота. Это в 2 раза больше, чем вишнёвого компота. Сколько банок вишнёвого компота заготовила на зиму тётя Люся?4. На первой улице строители выстроили 8 новых домов. Это в 4 раза больше, чем они построили домов на второй улице. Сколько новых домов выстроили на второй улице?5. Масса арбуза 8 кг. Это в 4 раза больше, чем масса дыни. Какова масса дыни?6. На лугу паслось 64 коровы. Это в 8 раз больше, чем коз. Сколько коз паслось на лугу?7. Для украшения класса взяли 4 гирлянды с жёлтыми лампочками, что в 2 раза больше, чем с зелёными лампочками. Сколько гирлянд с зелёными лампочками взяли для украшения класса?8. В зоопарке живут 36 фламинго. Это в 4 раза больше, чем 9. На улице растёт 72 дерева. Это в 9 раз больше, чем в переулке. Сколько деревьев растёт в переулке? 10. На противне 24 пирожка с грибами. Это в 3 раза больше, чем пирожков с луком. Сколько пирожков с луком на противне?

Задачи нахождения числа по доли и доли по числу

1. У продавца было 32 воздушных шарика. 1/4 часть всех воздушных шариков продавец продал. Сколько воздушных шариков продавец продал?2. Масса арбуза 10 кг. Съели 1/2 часть арбуза. Сколько килограммов арбуза съели?3. В стакане было 240 г сахарного песка. 1/4 стакана сахарного песка израсходовали. Сколько граммов сахарного песка израсходовали?4. Мальчик начертил отрезок длиной 27 см. 1/3 отрезка мальчик раскрасил цветными фломастерами. Сколько сантиметров отрезка мальчик раскрасил?5. Длина ленты 50 м. Отрезали 1/5 часть ленты. Сколько метров ленты отрезали? 6. Бабушка купила 10 яиц. 1/2 часть всех яиц она сварила. Сколько яиц сварила бабушка?7. В корзинке было 16 грибов. 1/2 часть всех грибов использовали на приготовление грибного супа. Сколько грибов использовали на приготовление грибного супа?8. В вазе лежало 8 яблок. 1/4 часть всех яблок съели. Сколько яблок съели?9. На карусели 10 лошадок. 1/2 часть лошадок осталась свободной. Сколько свободных лошадок осталось на карусели?10. От станции до дачи дорога занимает 50 мин. 1/5 часть пути дачники проходят пешком. Сколько минут дачники идут пешком?

Контрольные работы по математике для 3 класса — Математика 3 класс — 3 класс

КОНТРОЛЬНАЯ РАБОТА  5

Цель: проконтролировать усвоение приёма деления с остатком и его проверку, знание порядка действий в выражениях, умение решать задачи.

I вариант

1. Выполните деление с остатком и проверку к нему.

75 : 8                        85 : 20                        51 : 7

2. Вставьте числа в «окошки», чтобы получились верные равенства.

3. Найдите значения выражений.

56 : 2 – 36 : 12                                (39 + 33) : 24 · 9

48 + 32 : (64 : 8)                         93 – 3 · 8 : 6

4. Решите задачу.

Стекольщику нужно было вставить 96 стёкол. Он уже вставил в 14 окон по 3 стекла в каждое. Сколько стёкол осталось вставить стекольщику?

5. Решите задачу.

На тарелке было 48 блинов. Сколько блинов съели, если на тарелке осталось в 3 раза меньше блинов, чем было?

II вариант

1. Выполните деление с остатком и проверку к нему.

57 : 8                        74 : 7                        69 : 20

2. Вставьте числа в «окошки», чтобы получились верные равенства.

3. Найдите значения выражений.

80 + (24 – 4 · 5)                                42 : 3 + 72 : 24

78 – 8 · 8 : 2                                        24 + 36 : (54 : 9)

4. Решите задачу.

В большой корзине было 95 тюльпанов. Продавец сделал из них 12 букетов, по 7 тюльпанов в каждом букете. Сколько осталось тюльпанов?

5. Решите задачу.

На столе стояло 52 стакана с соком. Сколько стаканов с соком выпили, если на столе осталось в 4 раза меньше стаканов с соком, чем было первоначально?

КОНТРОЛЬНАЯ РАБОТА  6

Цели: проверить усвоение нумерации трёхзначных чисел; проверить усвоение вычислительных приёмов; проконтролировать навыки решения задач, построения отрезков.

I вариант

1. а) Вставьте в «окошки» пропущенные числа.

б) Запишите цифрами:

9 сот. 2 дес.                                8 сот.

4 сот. 3 ед.                                5 сот. 1 дес. 7 ед.

в) Представьте числа в виде суммы разрядных слагаемых.

510, 742.

2. Решите задачу.

3 набора красок стоят 72 рубля. Сколько стоят 4 таких набора красок?

3. Решите примеры.

549 + 1                        702 – 700                        60 : (26 + 4) · 2

800 – 1                        930 – 600                        42 + 54 : 3 · 2

600 + 50                        320 + 70                        71 – (28 – 17) · 6

4. Заполните пропуски нужными числами.

5. Начертите отрезок АВ = 6 см, а отрезок ВС в 2 раза длиннее. На сколько см длина отрезка ВС больше длины отрезка АВ?

II вариант

1. а) Вставьте в «окошки» пропущенные числа.

б) Запишите цифрами:

7 сот.                                5 сот 7 дес.

4 сот. 2 дес. 3 ед.                6 сот. 9 ед.

в) Представьте числа в виде суммы разрядных слагаемых.

490, 351.

2. Решите задачу.

72 стула расставили в 6 рядов, поровну в каждый ряд. Сколько стульев в 4 таких рядах?

3. Решите примеры.

659 + 1                        805 – 800                        96 : (41 – 9) · 3

900 – 1                        760 – 500                        36 + 60 : 4 · 2

400 + 80                        980 – 30                        72 – (44 + 16) : 4

4. Заполните пропуски нужными числами.

5. Начертите отрезок СД = 9 см, а отрезок АК в 3 раза короче. На сколько см длина отрезка СД больше длины отрезка АК?

КОНТРОЛЬНАЯ РАБОТА  7

Цель: проверить сформированность умений:

1) записывать и сравнивать трёхзначные числа;

2) складывать и вычитать трёхзначные числа;

3) решать задачи;

4) сравнивать единицы длины.

I вариант

1. а) Запишите число, в котором:

5 ед. III разряда и 2 ед. I разряда

7 ед. II разряда и 3 ед. I разряда

4 ед. III разряда

6 ед. III разряда и 9 ед. II разряда

б) Сравните числа:

567 … 601           300 … 299           110 … 101

2. Сравните (>, <, =).

5 м 4 дм … 540 см                        8 м 1 см … 8 м 1 дм

9 дм 2 см … 1 м                        604 см … 4 м 6 см

3. Решите примеры.

640 : 8 =                                 240 : 6 =

150 – 70 =                         560 : 8 =

440 : 20 =                        80 · 5 =

80 + 40 =                        20 · 6 =

4. Решите задачу.

В соревнованиях участвуют 310 мальчиков и 270 девочек. Гимнастов среди них было 250 человек, а остальные пловцы. Сколько пловцов участвуют в соревнованиях?

5. Решите примеры столбиком.

535 + 65                        756 – 628

198 + 672                963 – 817

189 + 467                707 – 629

II вариант

1. а) Запишите число, в котором:

9 ед. III разряда

7 ед. III разряда и 4 ед. II разряда

5 ед. II разряда и 2 ед. I разряда

8 ед. III разряда и 6 ед. I разряда

б) Сравните числа:

401 … 386           699 … 700           220 … 202

2. Сравните (>, <, =).

702 см … 2 м 7 см                        6 м 9 дм … 690 см

8 дм 3 см … 1 м                        4 м 5 см … 4 м 5 дм

3. Решите примеры.

630 : 7 =                                 90 + 7 =

210 : 3 =                                560 : 4 =

2 · 70 =                                360 : 4 =

170 – 80 =                         30 · 5 =

4. Решите задачу.

В музей поехали 250 первоклассников и 320 второклассников. Мальчиков среди них было 300 человек. Сколько девочек поехало в музей?

5. Решите примеры столбиком.

652 + 265                        683 – 134

363 + 498                        712 – 243

548 + 152                        622 – 355

Задачи по математике для 3 класса

Задача 2

• а) Как называют множество овец?
• б) Как называют множество лошадей?
• в) Как называют множество пчел, летящих вместе?
• г) Как называют множество футболистов, собравшихся вместе для игры? Какие еще командные игры ты знаешь?
• д) Как называют множество кораблей, плывущих вместе?
• е) Какие имеются названия для множеств военных?

Задача 4

Назови двух учеников твоего класса. Элементами какого множе-ства они являются? Принадлежат ли этому множеству портфели учеников?

Задача 6

На рисунке изображена семья Ивановых:

Покажи на этом рисунке множество детей и множество взрослых. Из каких элементов они состоят? Как будут звать Петю, когда он вырастет? Как будут звать Аню? Чьим отцом является Сергей Васильевич? Чьей бабушкой является Ирина Семеновна?

Задача 7

По какому признаку подобраны слова: роза, фиалка, гвоздика, василёк, тюльпан? Какие ещё элементы входят в это множество? Можно ли в пего включить сосну, барана, ромашку, шипы от розы? Какие цветы растут на клумбах? Какие растут в поле? Какие растут на лугу?

Задача 8

С каких деревьев взяты эти листья? Назови ещё 3 элемента множества деревьев. Всегда ли на деревьях есть листья? У всех ли деревьев есть листья?

Задача 9

Какое множество изображено на рисунке. В каких из этих плодов одно семечко или одна косточка, а в каких — много семян или косточек? Все ли плоды растут на деревьях? Что ещё растёт на дереве, кроме плодов?

• Реши задачи. Об элементах каких множеств в них идёт речь?

• а) Ласточка пролетает в час 40 км, а стриж — в 3 раза больше. Сколько километров в час пролетает стриж?
• б) Сосна живёт примерно 400 лет. Это на 250 лет больше, чем живёт липа. Сколько лет живёт липа?
• в) Для нормальной жизни рыбок скалярий им требуется но 3 л воды на каждую. Сколько рыбок могут жить в аквариуме, вмещающем 24 л воды?
• г) Масса пингвина-папы 42 кг, пингвина-мамы — 32 кг, а их детёныша — 8 кг. Какова масса всей пингвиньей семьи? На сколько папа тяжелее, чем мама с детёнышем вместе?

Пират нашёл клад из 900 монет. Чтобы побыстрее его унести, он положил 186 монет в шапку, 215 — в карман, 74 монеты запихнул в рот, 125 положил в правую ладонь, а 68— в левую. Сколько монет он не смог унести?

Составь программу действий и вычисли:

• а) 21 : 3 • 6 — (18 + 14) : 8
• б) 63 : (3 • 3) + (8 • 7 — 2) : 6

Два мальчика, Дима и Миша, отправились в булочную. По дороге они нашли 20 рублей. Сколько бы денег нашёл один Дима, если бы отправился в булочную?

На странице использованы задачи и задания из книги Л. Г. Петерсон «Математика. 3 класс. Часть1.» 2008г.
Ссылка на сайт автора: www.sch2000.ru

Простые задачи на нахождение цены

1. 6 одинаковых мочалок для посуды стоят 12 руб. Сколько стоит одна мочалка для посуды?2. 2 пачки хлебцев стоят 16 руб. Узнай цену пачки хлебцев. 3. 2 одинаковые расчёски для волос стоят 18 руб. Сколько стоит одна расчёска?4. Папа за 8 л бензина заплатил 72 руб. Сколько стоит 1 л бензина?5. За 3 одинаковые нити мишуры заплатили 30 руб. Узнай цену одной нити мишуры. 6. Тётя Люся за 5 пакетов сливок заплатила 50 руб. Узнай цену одного пакета сливок.7. 4 банки майонеза стоят 36 руб. Сколько стоит одна банка майонеза?8. За 3 банки томатной пасты заплатили 12 руб. Сколько стоит одна банка томатной пасты?9. За 7 электрических лампочек заплатили 42 руб. Сколько стоит одна электрическая лампочка?10. За 2 одинаковых фляжки для воды заплатили 16 руб. Сколько стоит одна фляжка?

Деление с остатком

Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.

Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.

Урок может выглядеть так:

1. Расскажите ученику третьего класса, что не все цифры можно поделить поровну. Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
2. Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).

Группировка нот

Группировкой называется объединение нот в группы. Это делается с одной простой целью – облегчить визуальное восприятие нот и ускорить разбор ритмического рисунка. Для сравнения приведу пример в виде номера телефона. Какой вариант легче воспринимать? Думаю, вы согласитесь, что второй:

Объединяться в группы могут только длительности с флажками, то есть длительности меньше четверти – восьмые, шестнадцатые и так далее. Когда они соединяются в группу, то флажки нот превращаются в горизонтальные линии — ребра. Сколько было флажков, столько будет и ребер у группы:

В группы могут объединяться ноты разной продолжительности, главное, чтобы все они были меньше четверти. Пусть вас не смущает разное количество флажков, это вовсе не мешает объединять ноты в группы:

Также паузы могут встраиваться в группу:

Группировка длительностей в такте

Рассмотрим пример группировки нот в самых популярных размерах: 2/4, 3/4, 4/4, 6/8.

В размерах 2/4, 3/4, 4/4 ноты объединяются в группы по счетным долям (они указаны в знаменателе размера) – в нашем случае это четверти. Группировать следует так, чтобы границы долей было отчетливо видно. Например, в размере 4/4 шестнадцатые ноты нужно группировать по четыре:

Не трудно посчитать, что каждая группа равна четвертной доле. В одном такте будет 4 таких группы.

А вот пример того, как группировать не следует:

Визуально воспринимать такую группировку нот чрезвычайно трудно, а читать с листа – невозможно.

Размер 4/4 — сложный и состоит из двух простых – 2/4 + 2/4. Поэтому иногда ноты в этом размере группируются не по долям, а в соответствии с составным простым размером. Получится две группы по две четверти. Как лучше сгруппировать ноты выбирает сам композитор, главное, чтобы это легко воспринималось глазами.

В размере 2/4 ноты объединяют в две группы, каждая из которых равна четверти:

Ниже приведен пример группировки в размере 3/4:

Ритмический рисунок не самый простой, но ноты сгруппированы таким образом, что сразу видно каждую долю и посчитать размер такта не составит труда.

В размерах 6/8, 9/8, 12/8 счёт осуществляется восьмыми нотами. Принцип группировки в таких размерах будет несколько другим. Эти размеры сложные трехдольные и, как вы уже знаете, состоят они из нескольких простых:

Группировать ноты в подобных случаях, следует опираясь на простой размер, из которого состоит сложный — в нашем случае это размер 3/8. Эти цифры служат нам подсказкой, говоря, что ноты нужно собирать в такие группы, где сумма длительностей будет равна трем восьмым. Например, в размере 6/8 (3/8+3/8) ноты нужно объединять в две группы по три восьмые в каждой.

Ритм может быть самым разнообразным, но каждая группа нот, все равно должна быть равны трем восьмым:

Группировка нот напрямую зависит от музыкального размера. Мы рассмотрели не все варианты группировки, но главное усвоить принцип и запомнить, что группировать нужно так, чтобы это было удобно читать.

Статья понравилась186Статья не понравилась99

Заключение

А сейчас посмотрите джазовую пьесу «Take Five«, записанную квартетом «The Dave Brubeck Quartet» в 1959 году. это был первый джазовый сингл, разошедшийся в более чем миллионе экземпляров. Автор пьесы — Paul Desmond, саксофонист квартета. Написана эта музыка в достаточно необычном ритме 5/4. Именно отсюда и идет ее название.

https://youtube.com/watch?v=tT9Eh8wNMkw%3F